5.3.2 Principle of Ferroelectricity: Energetics

The movement of central atom in the above structure can explained in terms of a potential energy diagram.

This situation can be explained in terms of a potential energy between two adjacent low energy sites. There are two equilibrium positions in which a B ion can stay, but to change from one state to another, energy must be provided to overcome an energy barrier ΔE. These energy wells further tilt to the left or right, depending upon the polarity of the electric field i.e. in the non-zero field state making on configuration more stable than another. However, a coercive field, which is the field required to bring the polarization back to zero, is needed when you switch to other direction of the field.

Ferroelectric materials follow Curie-Weiss law which is expressed as

(5.1)

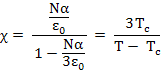Here, N is the number of dipoles per unit volume of the material, α is dipolar polarizability, and T_c is defined as the Ferroelectric transition temperature or the Curie temperature.

Ferroelectric behaviour is observed below the Curie Temperature above which the ferroelectric phase converts into a paraelectric phase which always has higher symmetry than the ferroelectric phase (for example transformation of low symmetry tetragonal BaTiO₃ to higher symmetry cubic BaTiO₃ at about 120^oC while heating) and ferroelectricity disappears. A paraelectric state is essentially a centrosymmetric higher symmetry state where dipoles are randomly oriented in a crystal giving rise to zero polarization.