where τ is defined as relaxation time.
Application of alternating fields to this polarization is not as simple as in the previous analysis
This is because the saturation polarization, Ps, is dependent on the instantaneous value of field and thus will be time-dependent and the local field is a function of both position and time.
In any case, if we assume that polarizing field is expressed as E* = E0 exp (1wt) then
Ps can be expressed as
 |
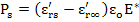(4.100) |
Here, we can define εrs' as static dielectric constant or dielectric constant at very low frequencies and εr∞' is dielectric constant at high frequencies covering electronic and ionic polarization. This kind of makes sense because dipolar polarization occurs between these two ends of the frequency.
Now, substitute E* and Ps into (4.98)
 |
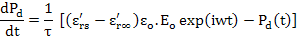(4.101) |
The integration of this equation yields us
 |
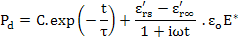(4.102) |
Here the first term is the transient time dependent term depicting decay of the d.c. charges on the capacitor and second term is the a.c. behavior of the polarization under an alternating field.
Since, electronic and ionic polarization are approximately frequency independent in this regime of frequencies, we can write
 |
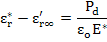(4.103) |
Now ignoring the transient time dependent term of (4.95) and substituting (4.96) into (4.94), we get
 |
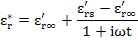(4.104) |
We also know that εr* = εr' - iεr'', hence, now we can separate the real and imaginary parts as
 |
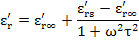(4.105a) |
 |
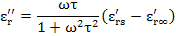(4.105b) |
and the loss tangent is
 |
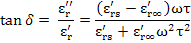(4.106) |
The above equations are called Debye equations.
The graphical representation of these is shown below:
| Figure 4.24 Graphical representation of Debye equations |
Here, the relaxation frequency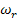 
is defined as inverse of the relaxation time i.e. 1/τ.
The equation (4.98) and the above figure suggest that εr' is independent of frequency at values corresponding to the sum of three polarizations i.e. Pd+Pi+Pe. As the applied field frequency approaches value ω = 1/τ, εr' passes an inflection and then drops off to εr∞' which is dependent only on (Pi+Pe).
At ω = 1/τ, the oscillating charges are coupled with the applied field and absorb maximum energy as depicted by the peak in εr'' magnitude of εr'' peak being (εrs'' - εr∞')/2 depending upon the number of oscillating charges and distance of motion.
It is also seen that tanδ is also goes than a maximum, but at higher frequencies with ω = (εrs'/εr∞')1/2/τ.
Now since, we have understood that polarization develops by temperature dependent diffusional processes which also give rise to the d.c. conductivity, temperature dependence of the relaxation time, τ can be expressed as
 |
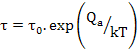(4.107) |
where Qa is the activation energy for dipole relaxation and τ0 is the intrinsic relaxation time.
Combining Debye equations with (4.99) we can obtain the frequencies (= ωτ) at which maxima for εr'' as well as tanδ occur and you will that these frequencies for the maxima change with temperature because τ is temperature dependent. The plots below show this trend for Li2O.2SiO2 glass ceramic.
| Figure 4.25 Shift of tanδ peak in Li2O.2SiO2 glass due to increasing temperature (Reproduced from Principle of Electronic Ceramics, L.L. Hench & J.K. West, P206) |
| Figure 4.26 Temperature dependence of the frequency maxima vs time for Li2O.2SiO2 glass at 500°C (Reproduced from Principle of Electronic Ceramics, L.L. Hench & J.K. West, P207) |
