|
4.8.1 Bi-stable model for dipolar relaxation
| Figure 4.23 Schematic of a polar molecule going one state to another and resulting energy well diagram |
In a solid when field is applied to a polar material, the ions hop from ionic position to another as shown above in figure 4.23, e.g. Na+ movement in glasses. We consider a bistable dipole model. As the cation moves from left to right, there is a change in the co-ordinates. At any temperature above 0K, there is random oscillation of cation between these sites.
The probability of jump between sites is given as
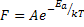 |
(4.92) |
Upon application of field, the wells tilt in the direction of applied field, resulting in unequal probability in two directions resulting a net flow of dipoles
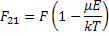 |
(4.93) |
where E is the applied field.
Under the application of an ac field, the change in the number of dipoles at site 1 = outflow to site 2 – inflow to site 1 i.e.
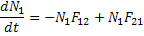 |
(4.94) |
Where N1 + N2 = N = constant
Further, since
Replace dN1/dt in the above equation, and we get
Now, polarization P can be expressed as the product of the net ions moved and the dipole moment i.e.
This is a relaxation equation with characteristic relaxation time τ=1/2F where F is the jump probability in s-1.
So, the above equation can be written as in the form of "Dipolar Polarization" by substituting P with Pd(t) and μ2/kT by dipolar polarizability leading to
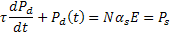 |
|
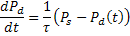 |
(4.98) |
Similar derivation can also be found in the Section 5.5 of the Chapter 5 of “Principles of Electronic Ceramics” by L.L. Hench and J.K. West. |