| |
4.8 Dipolar Relaxation i.e. Debye Relaxation in Polar Solids
Relaxation processes occur in many ceramics and ionic solids, especially glasses and these materials applying damped forced oscillator approach does not work in the low frequency region.
In such cases, the structure of the solid plays an important role because movement of charges may have to occur over many atomic distances and can be classified as diffusional in nature. These processes can be strongly temperature dependent in nature.
As a result, it may take considerable amount of time in the distribution of charges.
| Figure 4.21 Potential energy distribution of ionic sites in a glass |
For instance, in an ionic solid, application of a field leads to first almost instantaneous development of ionic and electronic polarization followed by slow development of dipolar polarization, Pd to a saturation polarization, Ps.
| Figure 4.22 Dependence of dipolar polarization on time |
We can approximately express the rate of change of polarization as
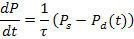 |
(4.91) |
where 1/τ is the proportionality constant. The above equation is also called Relaxation Equation. This equation can be derived using a simple bi-stable model in a similar fashion to that used in Module 3 (section 3.10) .
|
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
| |
|
|
|
|