4.6.3 Behavior of Real Dielectrics
However, in real dielectrics, the charging current is also accompanied by a loss current, associated with storage of electric charge by the dipoles. There are two sources of this loss current:
-
Long range migration of charges due to ohmic conduction and is frequency independent i.e. d.c. in nature, and
Dissipation of energy due to dipole rotation or oscillation as there always is certain inertial to their movement due their mass. This contribution is time-dependent i.e. frequency dependent.
Since, both of these current are in phase with the applied field, the loss current, Il, can be written as
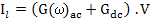 |
(4.59) |
where G depicts the conductance in mho or Siemens which is nothing but the inverse of resistance.
Hence, the total current, Il, is the sum of charging and loss current i.e
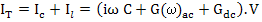 |
(4.60) |
Hence, the current in a real dielectric is a complex quantity that leads voltage by angle 90o- δ where δ is defined as the loss angle or dissipation factor. It is made up of two components that are 90° out of phase with respect to each other and have to be added vectorially as shown below. Naturally, δ will be zero if there was no loss current present.
| Figure 4.19 Real and Imaginary part of I and V |
When the field applied is static or d.c. i.e. ω = 0 then
where Gdc = 1/R and R is the ohmic resistance.
An alternative way to express the real dielectrics passing both charging and loss current is to use complex permittivity.
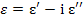 |
(4.61) |
and
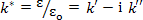 |
(4.62) |
Total current in a dielectric can now be expressed in terms of a single material parameter, k, since capacitance and charge are
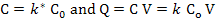 |
(4.63) |
Using equation (4.54), the total current can be expressed as
i.e.
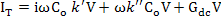 |
(4.65) |
Here
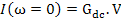 |
(4.66) |
The first term in (4.65) is the out-of-phase charging current term and last two terms are in-phase loss current terms.
Comparing equation (4.65) with (4.60) yields overall conductance, G, as
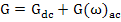 |
(4.67) |
where G(ω)ac = ωk''C0V
Loss tangent, tan δ, is expressed as
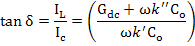 |
(4.68) |
If Gdc << ωk''C0 then
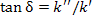 |
(4.69) |
The values of dielectric constant and loss tangent for selected materials are shown below.
| Material |
Dielectric Constant (εr') |
Loss Tangent (tanδ*10-4) |
Alumina |
10 |
5-20 |
SiO2 |
3.8 |
2 |
BaTiO3 |
500 |
150 |
Nylon |
3.1 |
10 |
Polycarbonate |
~3 |
10 |
PVC |
3 |
160 |
|