Uniform and Non-uniform Flows
The flow is defined as uniform flow when in the flow field the velocity and other hydrodynamic parameters do not change from point to
point at
any instant of time.
For a uniform flow, the velocity is a function of time only, which can be expressed in Eulerian description as
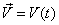
Implication:
- For a uniform flow, there will be no spatial distribution of hydrodynamic and other parameters.
- Any hydrodynamic parameter will have a unique value in the entire field, irrespective of whether it
changes with time − unsteady uniform flow OR
does not change with time − steady uniform flow.
- Thus ,steadiness of flow and uniformity of flow does not necessarily go together.
When the velocity and other hydrodynamic parameters changes from one point to another the flow is defined as
non-uniform.
Important points:
1. For a non-uniform flow, the changes with position may be found either in the direction of flow or in directions perpendicular to it.
2.Non-uniformity in a direction perpendicular to the flow is always encountered near solid boundaries past which the fluid flows.
Reason: All fluids possess viscosity which reduces the relative velocity
(of the fluid w.r.t. to the wall) to zero at a solid boundary. This is known as no-slip condition.
Four possible
combinations
|
Type |
Example |
|
1. Steady Uniform flow |
Flow at constant rate through a duct of uniform cross-section (The region close to the walls of the duct is disregarded) |
|
2. Steady non-uniform flow |
Flow at constant rate through a duct of non-uniform cross-section (tapering pipe) |
|
3. Unsteady Uniform flow |
Flow at varying rates through a long straight pipe of uniform cross-section. (Again the region close to the walls is ignored.) |
|
4. Unsteady non-uniform flow |
Flow at varying rates through a duct of non-uniform cross-section. |
|
|