|
Material Derivative and Acceleration
-
Let the position of a particle at any instant t in a flow field be given by the space coordinates (x, y, z) with respect to a rectangular cartesian frame of reference.
-
The velocity components u, v, w of the particle along x, y and z directions respectively can then be written in
Eulerian form as
u = u (x, y, z, t)
v = v (x, y, z, t)
w = w (x, y, z, t)
-
After an infinitesimal time interval t , let the particle move to a new position given by the coordinates (x + Δx, y +Δy , z + Δz).
-
Its velocity components at this new position be u + Δu, v + Δv and w +Δw.
-
Expression of velocity
components in the Taylor's series form:
The increment in space coordinates can be written as -
Substituting the values of 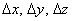 in above equations, we have in above equations, we have
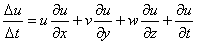 etc etc |
|
|