Perfect Gas
| |
where
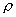 is the density (kg/m3 ). is the density (kg/m3 ).
|
- In another approach, which is particularly useful in chemically reacting systems, the equation of state is written as
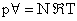 |
(38.9) |
where N is the number of moles in the system, and 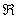 is the universal gas constant which is same for all gases is the universal gas constant which is same for all gases
.
|
- Recall that a mole of a substance
is that amount which contains a mass equal to the molecular
weight of the gas and which is identified with the
particular system of units being used. For example, in case
of oxygen (O2), 1 kilogram-mole (or kg. mol) has a mass of 32 kg. Because the masses of different molecules are in the same ratio as their molecular weights; 1 mol of different gases always contains the same number of molecules, i.e. 1 kg-mol always contains 6.02 ×1026 molecules, independent of the species of the gas. Dividing Eq. (38.9) by the number of moles of the system yields
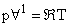 |
(38.10) |
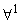 : Vol. per unit mole : Vol. per unit mole
If Eq. (38.9) is divided by the mass of the system, we can write
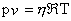 |
(38.11) |
where v is the specific volume as before and
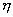 is the mole-mass ratio (kg- mol/kg). Also, Eq. (38.9) can be divided by system volume, which results in is the mole-mass ratio (kg- mol/kg). Also, Eq. (38.9) can be divided by system volume, which results in
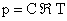 |
(38.12) |
where C is the concentration (kg - mol/m3 )
|
-
The equation of state can also be expressed in terms of particles. If
NA is the number of molecules in a mole (Avogadro constant, which for a kilogram- mole is
6.02 ×1026 particles), from Eq. (38.12) we obtain
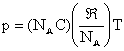 |
(38.13) |
|
In the above equation,
NAC is the number density, i.e. number of particles per unit volume and
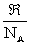 is the gas constant per particle, which is nothing but Boltzmann constant. is the gas constant per particle, which is nothing but Boltzmann constant.
Finally, Eq. (38.13) can be written as
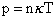 |
(38.14) |
where n: number density
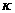 : Boltzmann constant. : Boltzmann constant.
|
- It is interesting to note that there exist a variety of gas constants whose use depends on the equation in consideration.
1.Universal gas constant- When the equation deals with moles, it is in use. It is same for all the gases.
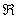 = 8314 J/( Kg-mol-K) = 8314 J/( Kg-mol-K) |
2.Characteristic gas constant- When the equation deals with mass, the characteristic gas constant (R) is used. It is a gas constant per unit mass and it is different for different gases. As such
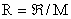 , where M is the molecular weight. For air at standard conditions, , where M is the molecular weight. For air at standard conditions,
3.Boltzmann constant- When the equation deals with molecules, Boltzmann constant is used. It is a gas constant per unit molecule .
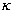 = 1.38 X 10 -23J / K = 1.38 X 10 -23J / K |
|
Application of the perfect gas theory
- It has been experimentally determined that at low pressures (1 atm or less) and at high temperature (273 K and above), the value of
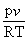 ( the well known compressibility z, of a gas) for most pure gases differs from unity by a quanity less than one percent ( the well known compressibility z, of a gas). ( the well known compressibility z, of a gas) for most pure gases differs from unity by a quanity less than one percent ( the well known compressibility z, of a gas).
- Also, that at very low temperatures and high pressures the molecules are densely packed. Under such circumstances, the gas is defined as real gas and the perfect gas equation of state is replaced by the famous Van-der-Waals equation which is
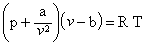 |
(38.15) |
|
where a and b are constants and depend on the type of the gas.
In conclusion, it can be said that for a wide range of applications related to compressible flows, the temperatures and pressures are such that the equation of state for the perfect gas can be applied with high degree of confidence.
|
|
|