Internal Energy and Enthalpy
|
- Microscopic view of a gas is a collection of particles in random motion. Energy of a particle consists of translational energy, rotational energy, vibrational energy and specific electronic energy. All these energies summed over all the particles of the gas, form the specific internal energy, e , of the gas.
|
-
Imagine a gas in thermodynamic equilibrium,i.e., gradients in velocity, pressure, temperature and chemical concentrations do not exist.
Then the enthalpy, h , is defined as
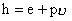 , where , where 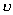 is the specific volume. is the specific volume.
If the gas is not chemically reacting and the intermolecular forces are neglected, the system can be called as a thermally perfect gas, where internal energy and enthalpy are functions of temperature only. One can write
|
For a calorically perfect gas,
|
Please note that in most of the compressible flow applications, the pressure and temperatures are such that the gas can be considered as calorically perfect.
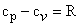 |
(38.19) |
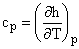 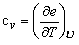 |
(38.20) |
|
Equation (38.19), can be rewritten as
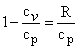 |
(38.21) |
Also
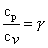 . So we can rewrite Eq. (38.21) as . So we can rewrite Eq. (38.21) as
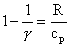 |
(38.22) |
|
In a similar way, from Eq. (38.19) we can write
 |
(38.23) |
|
|