-
Compressible flow is often called as variable density flow. For the flow of all liquids and for the flow of gases under certain conditions, the density changes are so small that assumption of constant density remains valid.
|
- Let us consider a small element of fluid of volume
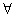 . The pressure exerted on the element by the neighbouring fluid is p . If the pressure is now increased by an amount dp , the volume of the element will correspondingly be reduced by the amount d . The pressure exerted on the element by the neighbouring fluid is p . If the pressure is now increased by an amount dp , the volume of the element will correspondingly be reduced by the amount d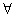 .The compressibility of the fluid K is thus defined as .The compressibility of the fluid K is thus defined as
|
However, when a gas is compressed, its temperature increases. Therefore, the above mentioned definition of compressibility is not complete unless temperature condition is specified. When the temperature is maintained at a constant level, the isothermal compressibility is defined as
|
-
Compressibility is a property of fluids. Liquids have very low value of compressibility (for ex. compressibility of water is 5 ´ 10-10 m2/N at 1 atm under isothermal condition), while gases have very high compressibility (for ex. compressibility of air is 10-5 m2/N at 1 atm under isothermal condition).
|
|
We can say that from Eqn (38.1) for a change in pressure, dp, the change in density is
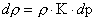
|
(38.4) |
|
| |
-
If we also consider the fluid motion, we shall appreciate that the flows are initiated and maintained by changes in pressure on the fluid. It is also known that high pressure gradient is responsible for high speed flow. However, for a given pressure gradient dp , the change in density of a liquid will be much smaller than the change in density of a gas (as seen in Eq. (38.4)).
|
So, for flow of gases, moderate to high pressure gradients lead to substantial changes in the density. Due to such pressure gradients, gases flow with high velocity. Such flows, where
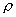 is a variable, are known as compressible flows. is a variable, are known as compressible flows.
|
- Recapitulating Chapter 1, we can say that the proper criterion for a nearly incompressible flow is a small Mach number,
where
V is the flow velocity and a is the speed of sound in the fluid. For small Mach number, changes in fluid density are small everywhere in the flow field.
|
- In this chapter we shall treat compressible flows which have Mach numbers greater than 0.3 and exhibit appreciable density changes. The Mach number is the most important parameter in compressible flow analysis. Aerodynamicists make a distinction between different regions of Mach number.
Categories of flow for external aerodynamics.
- Ma < 0.3: incompressible flow; change in density is negligible.
- 0.3< Ma < 0.8: subsonic flow; density changes are significant but shock waves do not appear.
- 0.8< Ma < 1.2: transonic flow; shock waves appear and divide the subsonic and supersonic regions of the flow. Transonic flow is characterized by mixed regions of locally subsonic and supersonic flow
- 1.2 < Ma < 3.0: supersonic flow; flow field everywhere is above acoustic speed. Shock waves appear and across the shock wave, the streamline changes direction discontinuously.
- 3.0< Ma : hypersonic flow; where the temperature, pressure and density of the flow increase almost explosively across the shock wave.
|
-
For internal flow, it is to be studied whether the flow is subsonic ( Ma < 1) or supersonic (Ma > 1). The effect of change in area on velocity changes in subsonic and supersonic regime is of considerable interest. By and large, in this chapter we shall mostly focus our attention to internal flows.
|