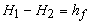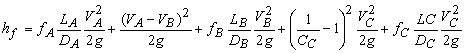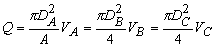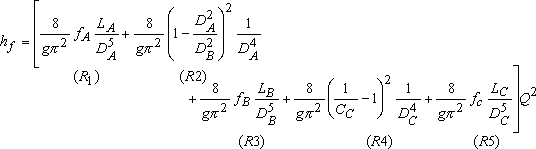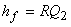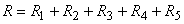Flow Through Branched Pipes
In several practical situations, flow takes place under a given head through different pipes jointed together either in series or in parallel or in a combination of both of them.
Pipes in Series
- If a pipeline is joined to one or more pipelines in continuation, these are said to constitute pipes in series. A typical example of pipes in series is shown in Fig. 36.1. Here three pipes A, B and C are joined in series.
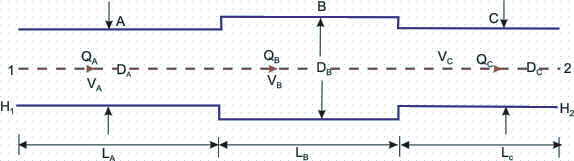
Fig 36.1 Pipes in series
In this case, rate of flow Q remains same in each pipe. Hence,
- If the total head available at Sec. 1 (at the inlet to pipe A) is
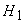 which is greater than which is greater than 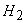 , the total head at Sec. 2 (at the exit of pipe C), then the flow takes place from 1 to 2 through the system of pipelines in series. , the total head at Sec. 2 (at the exit of pipe C), then the flow takes place from 1 to 2 through the system of pipelines in series.
-
Application of Bernoulli's equation between Secs.1 and 2 gives
where, 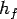 is the loss of head due to the flow from 1 to 2. Recognizing the minor and major losses associated with the flow, is the loss of head due to the flow from 1 to 2. Recognizing the minor and major losses associated with the flow, 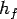 can be written as can be written as
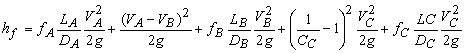 |
(36.1) |
| |
Friction loss
in pipe A |
Loss due to
enlargement at
entry to pipe B |
Friction loss
in pipe B |
Loss due
to abrupt
contraction
at entry
to pipe C |
Friction loss in
pipe C |
The subscripts A, B and C refer to the quantities in pipe A, B and C respectively. Cc is the coefficient of contraction.
- The flow rate Q satisfies the equation
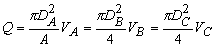 |
(36.2) |
Velocities VA, VB and VC in Eq. (36.1) are substituted from Eq. (36.2), and we get
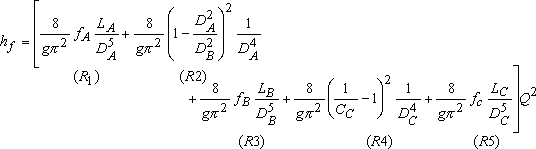 |
(36.3) |
|
|
|
(36.4) |
Equation (36.4) states that the total flow resistance is equal to the sum of the different resistance components. Therefore, the above problem can be described by an equivalent electrical network system as shown in Fig. 36.2.
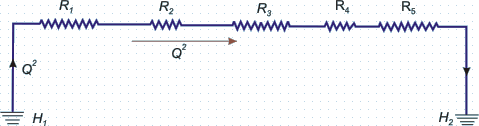
Fig 36.2 Equivalent electrical network system for through pipes in series
|

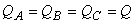
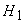 which is greater than
which is greater than 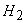 , the total head at Sec. 2 (at the exit of pipe C), then the flow takes place from 1 to 2 through the system of pipelines in series.
, the total head at Sec. 2 (at the exit of pipe C), then the flow takes place from 1 to 2 through the system of pipelines in series.