|
Skin Friction Coefficient For Boundary Layers On A Flat Plate
- Calculations of skin friction drag on lifting surface and on aerodynamic bodies are somewhat similar to the analyses of skin friction on a flat plate. Because of zero pressure gradient, the flat plate at zero incidence is easy to consider. In some of the applications cited above, the pressure gradient will differ from zero but the skin friction will not be dramatically different so long there is no separation.
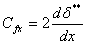 |
|
(34.26b) |
- Due to the similarity in the laws of wall, correlations of previous section may be applied to the flat plate by substituting
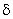 for R and for R and
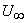 for the time mean velocity at the pipe centre.The rationale for using the turbulent pipe flow results in the situation of a turbulent flow over a flat plate is to consider that the time mean velocity, at the centre of the pipe is analogous to the free stream velocity, both the velocities being defined at the edge of boundary layer thickness. for the time mean velocity at the pipe centre.The rationale for using the turbulent pipe flow results in the situation of a turbulent flow over a flat plate is to consider that the time mean velocity, at the centre of the pipe is analogous to the free stream velocity, both the velocities being defined at the edge of boundary layer thickness.
Finally, the velocity profile will be [following Eq. (34.24)]
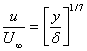 |
for 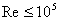 |
(34.27) |
Evaluating momentum thickness with this profile, we shall obtain
Consequently, the law of shear stress (in range of
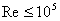 ) for the flat plate is found out by making use of the pipe flow expression of Eq. (34.24b) as ) for the flat plate is found out by making use of the pipe flow expression of Eq. (34.24b) as
Substituting
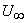 for for 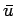 and and 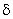 for R in the above expression, we get for R in the above expression, we get
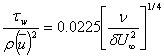 |
|
(34.29) |
Once again substituting Eqs (34.28) and (34.29) in Eq.(34.26), we obtain
|