• For simplicity, if we assume that the turbulent boundary layer grows from the leading edge of the plate we shall be able to apply the boundary conditions x = 0, δ = 0 which will yield C = 0, and Eq. (34.30) will become From Eqs (34.26b), (34.28) and (34.31), it is possible to calculate the average skin friction coefficient on a flat plate as

or,
or,	(34.31)
Where

From Eqs (34.26b), (34.28) and (34.31), it is possible to calculate the average skin friction coefficient on a flat plate as

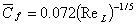(34.32)

It can be shown that Eq. (34.32) predicts the average skin friction coefficient correctly in the regime of Reynolds number below .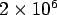

• This result is found to be in good agreement with the experimental results in the range of Reynolds number between 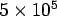and 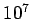which is given by
  
  

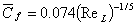  (34.33)

Equation (34.33) is a widely accepted correlation for the average value of turbulent skin friction coefficient on a flat plate.

• With the help of Nikuradse's experiments, Schlichting obtained the semi empirical equation for the average skin friction coefficient as

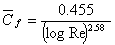(34.34)

Equation (34.34) was derived asssuming the flat plate to be completely turbulent over its entire length . In reality, a portion of it is laminar from the leading edge to some downstream position. For this purpose, it was suggested to use

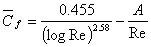(34.35a)

where A has various values depending on the value of Reynolds number at which the transition takes place.

• If the trasition is assumed to take place around a Reynolds number of 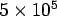, the average skin friction correlation of Schlichling can be written as

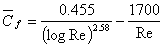(34.35b)

All that we have presented so far, are valid for a smooth plate.

• Schlichting used a logarithmic expression for turbulent flow over a rough surface and derived

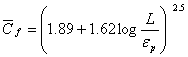(34.36)