|
Fully Developed Turbulent Flow In A Pipe For Moderate Reynolds Numbers
- The ratio of
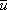 and and
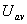 for the aforesaid profile is found out by considering the volume flow rate Q as for the aforesaid profile is found out by considering the volume flow rate Q as
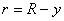
From equation (34.23)
or
or
or
or
- Now, for different values of
n (for different Reynolds numbers) we shall obtain different values of
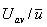 from Eq.(34.24a). On substitution of Blasius resistance formula (34.22) in Eq.(34.21), the following expression for the shear stress at the wall can be obtained. from Eq.(34.24a). On substitution of Blasius resistance formula (34.22) in Eq.(34.21), the following expression for the shear stress at the wall can be obtained.
putting 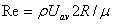
and where 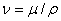
or
or
- For n=7,
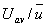 becomes equal to 0.8. substituting becomes equal to 0.8. substituting
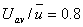 in the above equation, we get in the above equation, we get
Finally it produces
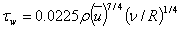 |
|
(34.24b) |
or
where
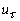 is friction velocity. However, is friction velocity. However,
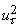 may be spitted into may be spitted into
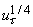 and and
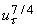 and we obtain and we obtain
or
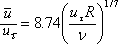 |
(34.25a) |
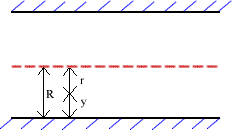
- Now we can assume that the above equation is not only valid at the pipe axis (y = R) but also at any distance from the wall y and a general form is proposed as
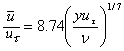 |
|
(34.25b) |
- It can be said that (1/7)th power velocity distribution law (24.38b) can be derived from Blasius's resistance formula (34.22) .
- Equation (34.24b) gives the shear stress relationship in pipe flow at a moderate Reynolds number, i.e
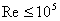 . Unlike very high Reynolds number flow, here laminar effect cannot be neglected and the laminar sub layer brings about remarkable influence on the outer zones. . Unlike very high Reynolds number flow, here laminar effect cannot be neglected and the laminar sub layer brings about remarkable influence on the outer zones.
- The friction factor for pipe flows,
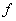 , defined by Eq. (34.22) is valid for a specific range of Reynolds number and for a particular surface condition. , defined by Eq. (34.22) is valid for a specific range of Reynolds number and for a particular surface condition.
|