- The boundary conditions as in Eg. (28.16), in combination with Eg. (28.21a) and (28.21b) become
at
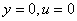 , therefore , therefore 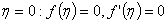 |
at
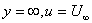 therefore therefore 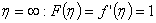
|
(28.23) |
Equation (28.22) is a third order nonlinear differential equation .
- Blasius obtained the solution of this equation in the form of series expansion through analytical techniques
- We shall not discuss this technique. However, we shall discuss a numerical technique to solve the aforesaid equation which can be understood rather easily.
- Note that the equation for
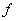 does not contain does not contain 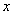 . .
- Boundary conditions at
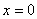 and and
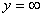 merge into the condition merge into the condition
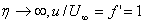 . This is the key feature of similarity solution. . This is the key feature of similarity solution.
- We can rewrite Eq. (28.22) as three first order differential equations in the following way
- Let us next consider the boundary conditions.
- The condition
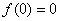 remains valid. remains valid.
- The condition
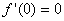 means that means that
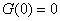 . .
- The condition
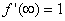 gives us gives us
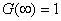 . .
Note that the equations for f and G have initial values. However, the value for H(0) is not known. Hence, we do not have a usual initial-value problem.
Shooting Technique
We handle this problem as an initial-value problem by choosing values of
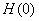 and solving by numerical methods and solving by numerical methods
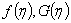 , and , and
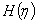 . .
In general, the condition
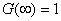 will not be satisfied for the function will not be satisfied for the function
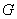 arising from the numerical solution. arising from the numerical solution.
We then choose other initial values of
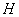 so that eventually we find an so that eventually we find an
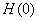 which results in which results in
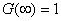 . .
This method is called the shooting technique .
-
In Eq. (28.24), the primes refer to differentiation wrt. the similarity variable
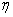 . The integration steps following Runge-Kutta method are given below.
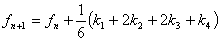 |
(28.25a) |
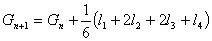 |
(28.25b) |
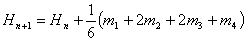 |
(28.25c) |
- One moves from
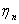 to to
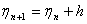 . A fourth order accuracy is preserved if h is constant along the integration path, that is, . A fourth order accuracy is preserved if h is constant along the integration path, that is,
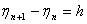 for all values of n . The values of k, l and m are as follows. for all values of n . The values of k, l and m are as follows.
- For generality let the system of governing equations be
In a similar way K3, l3, m3 and k4, l4,
m4 mare calculated following standard formulae for the Runge-Kutta integration. For example, K3 is given by
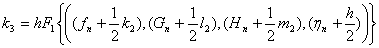 The functions F1, F2and F3 are G, H , - f H / 2 respectively. Then at a distance The functions F1, F2and F3 are G, H , - f H / 2 respectively. Then at a distance
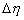 from the wall, we have from the wall, we have
- As it has been mentioned earlier
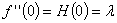 is unknown. It must be determined such that the condition is unknown. It must be determined such that the condition
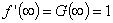 is satisfied. is satisfied.
The condition at infinity is usually approximated at a finite value of
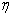 (around (around
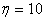 ). The process of obtaining ). The process of obtaining
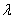 accurately involves iteration and may be calculated using the procedure described below. accurately involves iteration and may be calculated using the procedure described below.
- For this purpose, consider Fig. 28.2(a) where the solutions of
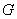 versus versus
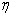 for two different values of for two different values of 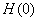 are plotted. are plotted.
The values of
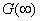 are estimated from the are estimated from the
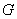 curves and are plotted in Fig. 28.2(b). curves and are plotted in Fig. 28.2(b).
- The value of
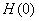 now can be calculated by finding the value now can be calculated by finding the value
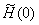 at which the line 1-2 crosses the line at which the line 1-2 crosses the line
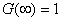 By using similar triangles, it can be said that By using similar triangles, it can be said that
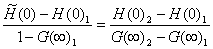 . By solving this, we get . By solving this, we get
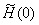 . .
- Next we repeat the same calculation as above by using
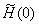 and the better of the two initial values of and the better of the two initial values of
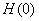 . Thus we get another improved value . Thus we get another improved value
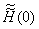 . This process may continue, that is, we use . This process may continue, that is, we use
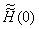 and and
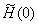 as a pair of values to find more improved values for as a pair of values to find more improved values for
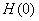 , and so forth. The better guess for H (0) can also be obtained by using the Newton Raphson Method. It should be always kept in mind that for each value of , and so forth. The better guess for H (0) can also be obtained by using the Newton Raphson Method. It should be always kept in mind that for each value of
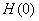 , the curve , the curve
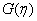 versus versus
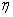 is to be examined to get the proper value of is to be examined to get the proper value of
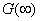 . .
- The functions
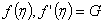 and and 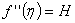 are plotted in Fig. 28.3.The velocity components, u and v inside the boundary layer can be computed from Eqs (28.21a) and (28.21b) respectively. are plotted in Fig. 28.3.The velocity components, u and v inside the boundary layer can be computed from Eqs (28.21a) and (28.21b) respectively.
- A sample computer program in FORTRAN follows in order to explain the solution procedure in greater detail. The program uses Runge Kutta integration together with the Newton Raphson method
Download the program
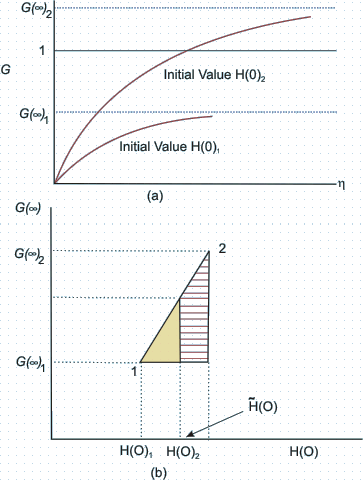 Fig 28.2 Correcting the initial guess for H(O)
Fig 28.2 Correcting the initial guess for H(O)
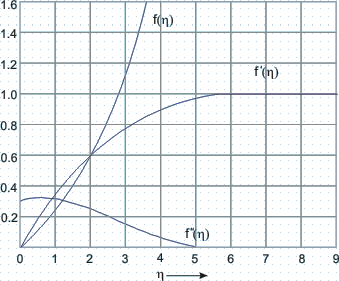 Fig 28.3 f, G and H distribution in the boundary layer
Fig 28.3 f, G and H distribution in the boundary layer
- Measurements to test the accuracy of theoretical results were carried out by many scientists. In his experiments, J. Nikuradse, found excellent agreement with the theoretical results with respect to velocity distribution
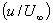 within the boundary layer of a stream of air on a flat plate. within the boundary layer of a stream of air on a flat plate.
- In the next slide we'll see some values of the velocity profile shape
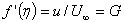 and and
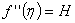 in tabular format. in tabular format.
|