|
Source or Sink
Source flow -
-
A flow with straight streamlines emerging from a point.
-
Velocity along each streamline varies inversely with distance from the point (shown in Fig.
20.3).
-
Only the radial component of velocity is non-trivial. (vθ=0, vz=0 ).
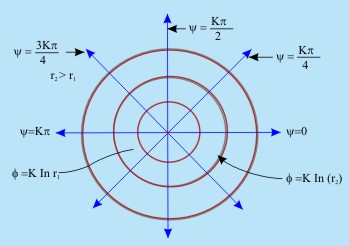
Fig 20.3 Flownet for a source flow
In a steady source flow the amount of fluid crossing any given cylindrical surface of radius r and unit length is constant (
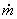 ) )
that is ( 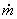 )in= ( )in= (
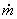 )out )out
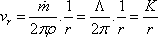 |
(20.10a) |
(which shows that velocity is inversely proportional to the distance )
where, K is the source strength
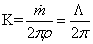 and and
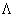 is the volume flow rate is the volume flow rate
The definition of stream function in cylindrical polar coordinate states that
 |
(20.11) |
For the source flow,
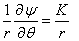 |
(20.12) |
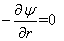 |
(20.13) |
Combining Eqs (20 .12) and (20.13) , we get
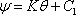 |
(20.14) |
Thus
Because the flow is irrotational, we can write
The integration constants C1 and C2 in Eqs (20.14) and (20.15) have no effect on the basic structure of velocity and pressure in the flow.
The equations for streamlines and velocity potential lines for source flow become
 |
(20.16) |
K = source strength and is proportional to
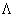
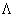 = the rate of volume flow from the source per unit depth perpendicular to the page = the rate of volume flow from the source per unit depth perpendicular to the page |
Sink flow
-
When
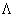 is negative , we get sink flow, is negative , we get sink flow,
-
here the flow is in the opposite direction of the source flow.
In Fig. 20.3, the point 0 is the origin of the radial streamlines. We visualize that point O is a point source or sink that induces radial flow in the
neighbourhood .
The point source or sink is a point of singularity in the flow field (because vr becomes infinite).
The stream function and velocity potential function are
 |
(20.17) |
End of Lecture 20!
To start next lecture click next button or select from left-hand-side.
|
|