|
Concept of Circulation in a Free Vortex Flow
Free Vortex Flow
-
Fluid particles move in circles about a point.
-
The only non-trivial velocity component is tangential.
-
This tangential speed varies with radius r so that same circulation is maintained.
-
Thus,all the streamlines are concentric circles about a given point where the velocity along each streamline is inversely proportional to the distance from the centre. This flow is necessarily irrotational.
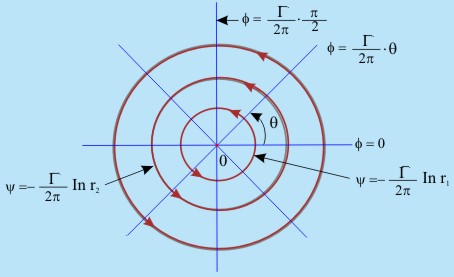
Fig 21.1 Flownet for a vortex (free vortex)
Velocity components
In a purely circulatory (free vortex flow) motion, the tangential velocity can be written as
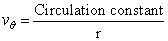 |
|
| or, |
|
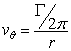 where where  is circulation is circulation |
(21.1) |
For purely circulatory motion we can also write
 |
(21.2) |
Stream Function
Using the definition of stream function, we can write
Combining Eqs (21.1) and (21.2) with the above said relations for stream function, it is possible to write
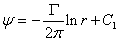 |
(21.3) |
Velocity Potential Function
Because of irrotationality, it should satisfy
Eqs (21.1) and (21.2) and the above solution of Laplace's equation yields
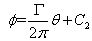 |
(21.4) |
Since, the integration constants C1 and C2 have no effect on the structure of velocities or pressures in the flow. We can ignore the integration constants without any loss of generality.
It is clear that the streamlines for vortex flow are circles while the potential lines are radial . These are given by
 |
(21.5) |
- In Fig. 21.1, point 0 can be imagined as a point vortex that induces the circulatory flow around it.
- The point vortex is a singularity in the flow field (vθ becomes infinite).
- Point 0 is simply a point formed by the intersection of the plane of a paper and a line perpendicular to the plane.
- This line is called vortex filament of strength
 where where  is the circulation around the vortex filament . is the circulation around the vortex filament .
Circulation is defined as
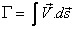 |
(21.6) |
This circulation constant denotes the algebraic strength of the vortex filament contained within the closed curve. From Eq. (21.6) we can write
For a two-dimensional flow
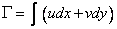 |
|
| or,
|
|
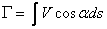 (according to Fig. 21.2) (according to Fig. 21.2) |
(21.7) |
Consider a fluid element as shown in Fig. 21.2. Circulation is positive in the anticlockwise direction (not a mandatory but general convention).
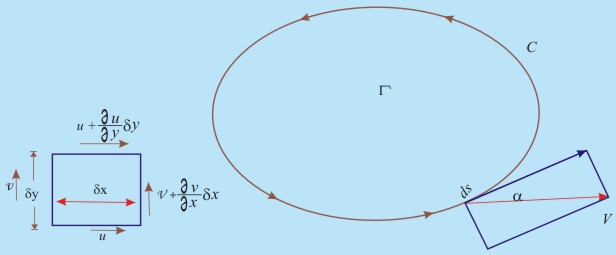
Fig 21.2 Circulation in a flow field
After simplification
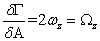 |
(21.8) |
Physically, circulation per unit area is the vorticity of the flow .
Now, for a free vortex flow, the tangential velocity is given by Eq. (21.1) as
For a circular path (refer Fig.21.2)
Thus,
Therefore
It may be noted that although free vortex is basically an irrotational motion, the circulation for a given path containing a singular point (including the origin) is constant (2πC) and independent of the radius of a circular streamline.
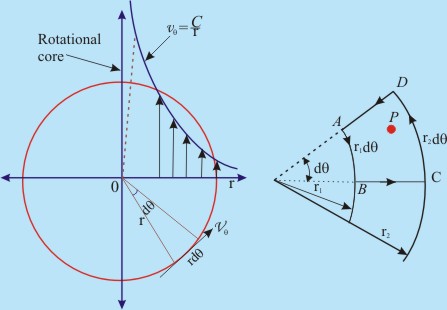
Fig 21.3 (a) Free Vortex Flow
Considering Fig 21.3 (a) and taking a closed contour ABCD in order to obtain circulation about the point, P around ABCD it may be shown that
|