Uniform Flow

• Velocity does not change with y-coordinate

• There exists only one component of velocity which is in the x direction.

• Magnitude of the velocity is U₀ .

Since  

or,
Thus,
	(20.4)

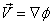
Using stream function ψ for  uniform flow

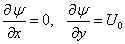so
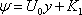	(20.5)

The constants of integration C₁ and K₁   are arbitrary.

 The values of ψ and Φ for different streamlines and velocity potential lines may change but flow pattern is unaltered

. The constants of integration may be omitted, without any loss of generality and it is possible to write

(20.6)

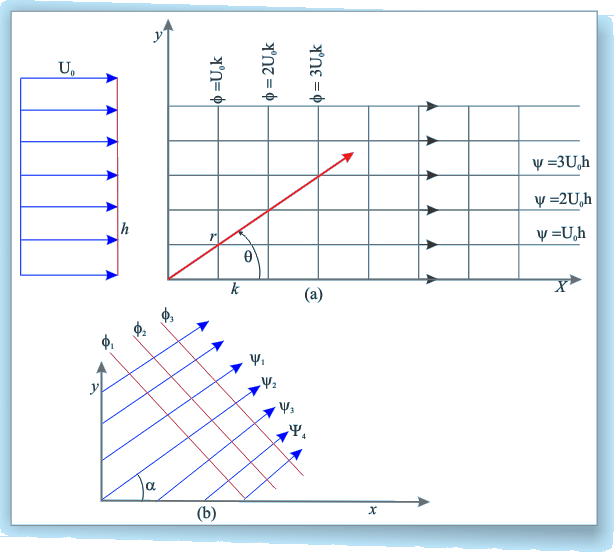
Fig 20..2          (a)  Flownet for a Uniform Stream        (b)     Flownet for uniform Stream with an Anglea with x-axis

These are plotted in Fig. 20.2(a) and consist of a rectangular mesh of straight streamlines and orthogonal straight potential-lines (remember streamlines and potential lines are always orthogonal ). It is conventional to put arrows on the streamlines showing the direction of flow.

In terms of polar (r - θ) coordinate, Eq. (20.6) becomes

(20.7)

Flow at an angle

If we consider a uniform stream at an angle α to the x-axis as shown in Fig. 20.2b. we require that

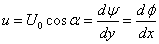and
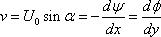	(20.8)

Integrating. we obtain for a uniform velocity U₀ at an angle α, the stream function and velocity potential respectively as

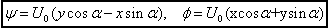(20.9)