|
Potential Flow Theory
Let us imagine a pathline
of a fluid particle shown in Fig. 20.1.
Rate of spin of the particle
is
ωz . The flow in which this spin is zero throughout is
known as irrotational flow .
For irrotational flows,
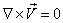
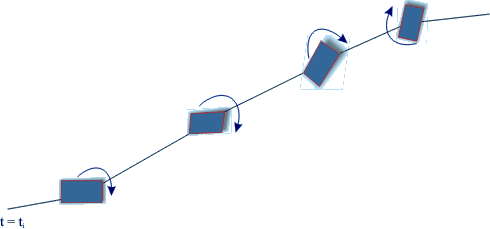
Fig 20.1 Pathline
of a Fluid Particle
Velocity Potential and
Stream Function
Since for irrotational flows
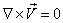 . .
the velocity for an irrotational flow, can be expressed as the gradient
of a scalar function called the velocity potential, denoted
by Φ
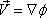 |
(20.2) |
Combination of Eqs (20.1)
and (20.2) yields
 |
(20.3) |
For irrotational flows
For two-dimensional case (as
shown in Fig 20.1)
which is again Laplace's equation.
-
From Eq. (20.3) we see
that an inviscid, incompressible, irrotational
flow is governed by Laplace's equation.
-
Laplace's equation is
linear, hence any number of particular solutions of Eq.(20.3)
added together will yield another solution .
-
A complicated flow pattern
for an inviscid, incompressible, irrotational flow can
be synthesized by adding together a number of elementary
flows ( provided they are also inviscid, incompressible
and irrotational)----- The
Superposition Principle
The analysis of Laplace's
Eq. (20.3) and finding out the potential functions are known
as Potential Flow Theory and the inviscid, incompressible,
irrotational flow is often called as Potential Flow .
There are some elementary
flows which constitute several complex potential-flow problems.

|