|
Analysis of Inviscid, Incompressible, Irrotation Flows
Incompressible flow is a constant density flow.
Let us visualize a
fluid element of defined mass, moving along a streamline in
an incompressible flow.
Due to constant density
, we can write
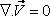 |
(20.1) |
Irrotational Flow
-
if the fluid
element does not rotate as it moves along the streamline, or
to be precise, if its motion is translational (and
deformation with no rotation) only,
the flow is termed as irrotational.
The rate of rotation
of the fluid element can be measured as the average
rate of rotation of two perpendicular line segments.
The average rate of
rotation ωz about z-axis is expressed in terms of the gradients
of velocity components as
Similarly, the other two
components of rotation are
ωx ,
ωy and
ωz are components
of
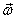
In a two-dimensional flow,
ωz is the only non-trivial component of the rate of rotation
called in-plane component of vorticity and computed as
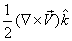
Thus for
irrotational flow, vorticity is zero i.e.
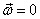
|