Equation (35.5) and (35.4) are also shown in Fig. 35.1 (curves III and IV) as the characteristics of losses in a centrifugal pump. By subtracting the sum of the losses from the head in consideration of the slip, at any flow rate (by subtracting the sum of ordinates of the curves III and IV from the ordinate of the curve II at all values of the abscissa), we get the curve V which represents the relationship of the actual head with the flow rate, and is known as head-discharge characteristic curve of the pump.
Effect of blade outlet angle
The head-discharge characteristic of a centrifugal pump depends (among other things) on the outlet angle of the impeller blades which in turn depends on blade settings. Three types of blade settings are possible (i) the forward facing for which the blade curvature is in the direction of rotation and, therefore, 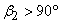 (Fig. 35.2a), (ii) radial, when (Fig. 35.2a), (ii) radial, when 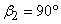 (Fig. 35.2b), and (iii) backward facing for which the blade curvature is in a direction opposite to that of the impeller rotation and therefore, (Fig. 35.2b), and (iii) backward facing for which the blade curvature is in a direction opposite to that of the impeller rotation and therefore, 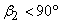 (Fig. 35.2c). The outlet velocity triangles for all the cases are also shown in Figs. 35.2a, 35.2b, 35.2c. From the geometry of any triangle, the relationship between (Fig. 35.2c). The outlet velocity triangles for all the cases are also shown in Figs. 35.2a, 35.2b, 35.2c. From the geometry of any triangle, the relationship between 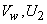 and and 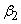 can be written as. can be written as.
which was expressed earlier by Eq. (35.2).
Figure 35.2 Outlet velocity triangles for different blade settings in a centrifugal pump |
In case of forward facing blade, 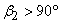 and hence cot and hence cot 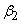 is negative and therefore is negative and therefore 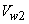 is more than is more than 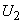 . In case of radial blade, . In case of radial blade, 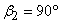 and and 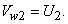 In case of backward facing blade, In case of backward facing blade, 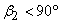 and and 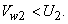 Therefore the sign of Therefore the sign of 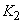 , the constant in the theoretical head-discharge relationship given by the Eq. (35.3), depends accordingly on the type of blade setting as follows: , the constant in the theoretical head-discharge relationship given by the Eq. (35.3), depends accordingly on the type of blade setting as follows:
For forward curved blades 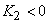
For radial blades 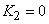
For backward curved blades 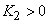
With the incorporation of above conditions, the relationship of head and discharge for three cases are shown in Figure 35.3. These curves ultimately revert to their more recognized shapes as the actual head-discharge characteristics respectively after consideration of all the losses as explained earlier Figure 35.4.
For both radial and forward facing blades, the power is rising monotonically as the flow rate is increased. In the case of backward facing blades, the maximum efficiency occurs in the region of maximum power. If, for some reasons, Q increases beyond 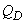 there occurs a decrease in power. Therefore the motor used to drive the pump at part load, but rated at the design point, may be safely used at the maximum power. This is known as self-limiting characteristic. In case of radial and forward-facing blades, if the pump motor is rated for maximum power, then it will be under utilized most of the time, resulting in an increased cost for the extra rating. Whereas, if a smaller motor is employed, rated at the design point, then if Q increases above there occurs a decrease in power. Therefore the motor used to drive the pump at part load, but rated at the design point, may be safely used at the maximum power. This is known as self-limiting characteristic. In case of radial and forward-facing blades, if the pump motor is rated for maximum power, then it will be under utilized most of the time, resulting in an increased cost for the extra rating. Whereas, if a smaller motor is employed, rated at the design point, then if Q increases above 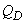 the motor will be overloaded and may fail. It, therefore, becomes more difficult to decide on a choice of motor in these later cases (radial and forward-facing blades). the motor will be overloaded and may fail. It, therefore, becomes more difficult to decide on a choice of motor in these later cases (radial and forward-facing blades).
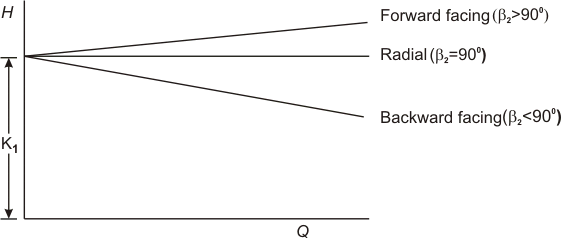 |
Figure 35.3 Theoretical head-discharge characteristic curves of a centrifugal pump for different blade settings |
Figure 35.4 Actual head-discharge and power-discharge characteristic curves of a centrifugal pump |
|