Flow through Volute Chambers
Apart from frictional effects, no torque is applied to a fluid particle once it has left the impeller. The angular momentum of fluid is therefore constant if friction is neglected. Thus the fluid particles follow the path of a free vortex. In an ideal case, the radial velocity at the impeller outlet remains constant round the circumference. The combination of uniform radial velocity with the free vortex ( 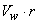 =constant) gives a pattern of spiral streamlines which should be matched by the shape of the volute. This is the most important feature of the design of a pump. At maximum efficiency, about 10 percent of the head generated by the impeller is usually lost in the volute. =constant) gives a pattern of spiral streamlines which should be matched by the shape of the volute. This is the most important feature of the design of a pump. At maximum efficiency, about 10 percent of the head generated by the impeller is usually lost in the volute.
Vanned Diffuser
A vanned diffuser, as shown in Fig. 36.1, converts the outlet kinetic energy from impeller to pressure energy of the fluid in a shorter length and with a higher efficiency. This is very advantageous where the size of the pump is important. A ring of diffuser vanes surrounds the impeller at the outlet. The fluid leaving the impeller first flows through a vaneless space before entering the diffuser vanes. The divergence angle of the diffuser passage is of the order of 8-10 ° which ensures no boundary layer separation. The optimum number of vanes are fixed by a compromise between the diffusion and the frictional loss. The greater the number of vanes, the better is the diffusion (rise in static pressure by the reduction in flow velocity) but greater is the frictional loss. The number of diffuser vanes should have no common factor with the number of impeller vanes to prevent resonant vibration.
Figure 36.1 A vanned diffuser of a centrifugal pump |
Cavitation in centrifugal pumps
Cavitation is likely to occur at the inlet to the pump, since the pressure there is the minimum and is lower than the atmospheric pressure by an amount that equals the vertical height above which the pump is situated from the supply reservoir (known as sump) plus the velocity head and frictional losses in the suction pipe. Applying the Bernoulli's equation between the surface of the liquid in the sump and the entry to the impeller, we have
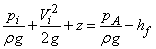 |
(36.1) |
where, 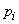 is the pressure at the impeller inlet and is the pressure at the impeller inlet and 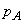 is the pressure at the liquid surface in the sump which is usually the atmospheric pressure, Z1 is the vertical height of the impeller inlet from the liquid surface in the sump, is the pressure at the liquid surface in the sump which is usually the atmospheric pressure, Z1 is the vertical height of the impeller inlet from the liquid surface in the sump, 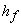 is the loss of head in the suction pipe. Strainers and non-return valves are commonly fitted to intake pipes. The term is the loss of head in the suction pipe. Strainers and non-return valves are commonly fitted to intake pipes. The term 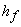 must therefore include the losses occurring past these devices, in addition to losses caused by pipe friction and by bends in the pipe. must therefore include the losses occurring past these devices, in addition to losses caused by pipe friction and by bends in the pipe.
In the similar way as described in case of a reaction turbine, the net positive suction head 'NPSH' in case of a pump is defined as the available suction head (inclusive of both static and dynamic heads) at pump inlet above the head corresponding to vapor pressure.
Therefore,
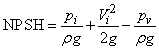 |
(36.2) |
Again, with help of Eq. (36.1), we can write
The Thomas cavitation parameter s and critical cavitation parameter 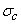 are defined accordingly (as done in case of reaction turbine) as are defined accordingly (as done in case of reaction turbine) as
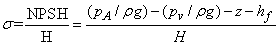 |
(36.3) |
and |
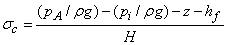 |
(36.4) |
We can say that for cavitation not to occur,
In order that s should be as large as possible, z must be as small as possible. In some installations, it may even be necessary to set the pump below the liquid level at the sump (i.e. with a negative vale of z ) to avoid cavitation. |