Characteristics of a Centrifugal Pump
With the assumption of no whirl component of velocity at entry to the impeller of a pump, the work done on the fluid per unit weight by the impeller is given by Equation( 34.2). Considering the fluid to be frictionless, the head developed by the pump will be the same san can be considered as the theoretical head developed. Therefore we can write for theoretical head developed 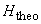 as as
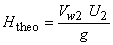 |
(35.1) |
From the outlet velocity triangle figure( 34.1)
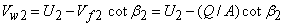 |
(35.2) |
where Q is rate of flow at impeller outlet and A is the flow area at the periphery of the impeller. The blade speed at outlet 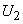 can be expressed in terms of rotational speed of the impeller N as can be expressed in terms of rotational speed of the impeller N as
Using this relation and the relation given by Eq. (35.2), the expression of theoretical head developed can be written from Eq. (35.1) as
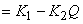 |
(35.3) |
where, 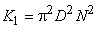 and and 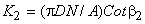
For a given impeller running at a constant rotational speed. 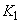 and and 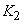 are constants, and therefore head and discharge bears a linear relationship as shown by Eq. (35.3). This linear variation of are constants, and therefore head and discharge bears a linear relationship as shown by Eq. (35.3). This linear variation of 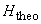 with Q is plotted as curve I in Fig. 35.1. with Q is plotted as curve I in Fig. 35.1.
If slip is taken into account, the theoretical head will be reduced to 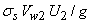 . Moreover the slip will increase with the increase in flow rate Q . The effect of slip in head-discharge relationship is shown by the curve II in Fig. 35.1. The loss due to slip can occur in both a real and an ideal fluid, but in a real fluid the shock losses at entry to the blades, and the friction losses in the flow passages have to be considered. At the design point the shock losses are zero since the fluid moves tangentially onto the blade, but on either side of the design point the head loss due to shock increases according to the relation . Moreover the slip will increase with the increase in flow rate Q . The effect of slip in head-discharge relationship is shown by the curve II in Fig. 35.1. The loss due to slip can occur in both a real and an ideal fluid, but in a real fluid the shock losses at entry to the blades, and the friction losses in the flow passages have to be considered. At the design point the shock losses are zero since the fluid moves tangentially onto the blade, but on either side of the design point the head loss due to shock increases according to the relation
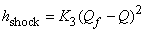 |
(35.4) |
Figure 35.1 Head-discharge characteristics of a centrifugal pump |
where 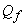 is the off design flow rate and is the off design flow rate and  is a constant. The losses due to friction can usually be expressed as is a constant. The losses due to friction can usually be expressed as
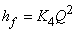 |
(35.5) |
where, 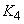 is a constant. is a constant.
|