Runner of the Francis Turbine
The shape of the blades of a Francis runner is complex. The exact shape depends on its specific speed. It is obvious from the equation of specific speed that higher specific speed means lower head. This requires that the runner should admit a comparatively large quantity of water for a given power output and at the same time the velocity of discharge at runner outlet should be small to avoid cavitation. In a purely radial flow runner, as developed by James B. Francis, the bulk flow is in the radial direction. To be more clear, the flow is tangential and radial at the inlet but is entirely radial with a negligible tangential component at the outlet. The flow, under the situation, has to make a 90o turn after passing through the rotor for its inlet to the draft tube. Since the flow area (area perpendicular to the radial direction) is small, there is a limit to the capacity of this type of runner in keeping a low exit velocity. This leads to the design of a mixed flow runner where water is turned from a radial to an axial direction in the rotor itself. At the outlet of this type of runner, the flow is mostly axial with negligible radial and tangential components. Because of a large discharge area (area perpendicular to the axial direction), this type of runner can pass a large amount of water with a low exit velocity from the runner. The blades for a reaction turbine are always so shaped that the tangential or whirling component of velocity at the outlet becomes zero 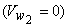 . This is made to keep the kinetic energy at outlet a minimum. . This is made to keep the kinetic energy at outlet a minimum.
Figure 29.1 shows the velocity triangles at inlet and outlet of a typical blade of a Francis turbine. Usually the flow velocity (velocity perpendicular to the tangential direction) remains constant throughout, i.e. 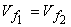 and is equal to that at the inlet to the draft tube. and is equal to that at the inlet to the draft tube.
The Euler's equation for turbine [Eq.(1.2)] in this case reduces to
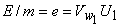 |
(29.1) |
where, e is the energy transfer to the rotor per unit mass of the fluid. From the inlet velocity triangle shown in Fig. 29.1
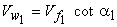 |
(29.2a) |
| and |
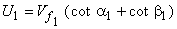 |
(29.2b) |
Substituting the values of 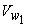 and and  from Eqs. (29.2a) and (29.2b) respectively into Eq. (29.1), we have from Eqs. (29.2a) and (29.2b) respectively into Eq. (29.1), we have
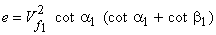 |
(29.3) |
Figure 29.1 Velocity triangle for a Francis runner |
The loss of kinetic energy per unit mass becomes equal to 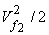 . Therefore neglecting friction, the blade efficiency becomes . Therefore neglecting friction, the blade efficiency becomes
The change in pressure energy of the fluid in the rotor can be found out by subtracting the change in its kinetic energy from the total energy released. Therefore, we can write for the degree of reaction.
[since 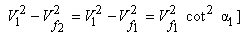 |
|