|
where 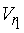 and and 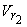 are the velocities of the jet relative to the bucket at its inlet and outlet and are the velocities of the jet relative to the bucket at its inlet and outlet and 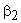 is the outlet angle of the bucket. is the outlet angle of the bucket.
From the Eq. (1.2) (the Euler's equation for hydraulic machines), the energy delivered by the fluid per unit mass to the rotor can be written as
| |
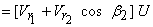 |
(26.1) |
(since, in the present situation, 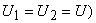
The relative velocity 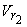 becomes slightly less than becomes slightly less than 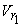 mainly because of the friction in the bucket. Some additional loss is also inevitable as the fluid strikes the splitter ridge, because the ridge cannot have zero thickness. These losses are however kept to a minimum by making the inner surface of the bucket polished and reducing the thickness of the splitter ridge. The relative velocity at outlet mainly because of the friction in the bucket. Some additional loss is also inevitable as the fluid strikes the splitter ridge, because the ridge cannot have zero thickness. These losses are however kept to a minimum by making the inner surface of the bucket polished and reducing the thickness of the splitter ridge. The relative velocity at outlet  is usually expressed as is usually expressed as 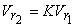 where, K is a factor with a value less than 1. However in an ideal case ( in absence of friction between the fluid and blade surface) K=1. Therefore, we can write Eq.(26.1) where, K is a factor with a value less than 1. However in an ideal case ( in absence of friction between the fluid and blade surface) K=1. Therefore, we can write Eq.(26.1)
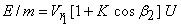 |
(26.2) |
If Q is the volume flow rate of the jet, then the power transmitted by the fluid to the wheel can be written as
| |
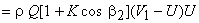 |
(26.3) |
The power input to the wheel is found from the kinetic energy of the jet arriving at the wheel and is given by 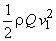 . Therefore the wheel efficiency of a pelton turbine can be written as . Therefore the wheel efficiency of a pelton turbine can be written as
| |
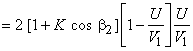 |
(26.4) |
It is found that the efficiency 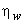 depends on depends on 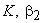 and and 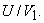 For a given design of the bucket, i.e. for constant values of For a given design of the bucket, i.e. for constant values of 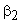 and K, the efficiency and K, the efficiency 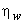 becomes a function of becomes a function of 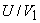 only, and we can determine the condition given by only, and we can determine the condition given by 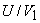 at which at which 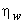 becomes maximum. becomes maximum.
For 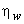 to be maximum, to be maximum,
| or, |
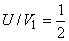 |
(26.5) |
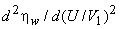 is always negative. is always negative.
Therefore, the maximum wheel efficiency can be written after substituting the relation given by eqn.(26.5) in eqn.(26.4) as
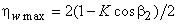 |
(26.6) |
|