KAPLAN TURBINE
Introduction
Higher specific speed corresponds to a lower head. This requires that the runner should admit a comparatively large quantity of water. For a runner of given diameter, the maximum flow rate is achieved when the flow is parallel to the axis. Such a machine is known as axial flow reaction turbine. An Australian engineer, Vikton Kaplan first designed such a machine. The machines in this family are called Kaplan Turbines.(Figure 30.1)
Figure 30.1 A typical Kaplan Turbine |
Development of Kaplan Runner from the Change in the Shape of Francis Runner with Specific Speed
Figure 30.2 shows in stages the change in the shape of a Francis runner with the variation of specific speed. The first three types [Fig. 30.2 (a), (b) and (c)] have, in order. The Francis runner (radial flow runner) at low, normal and high specific speeds. As the specific speed increases, discharge becomes more and more axial. The fourth type, as shown in Fig.30.2 (d), is a mixed flow runner (radial flow at inlet axial flow at outlet) and is known as Dubs runner which is mainly suited for high specific speeds. Figure 30.2(e) shows a propeller type runner with a less number of blades where the flow is entirely axial (both at inlet and outlet). This type of runner is the most suitable one for very high specific speeds and is known as Kaplan runner or axial flow runner.
From the inlet velocity triangle for each of the five runners, as shown in Figs (30.2a to 30.2e), it is found that an increase in specific speed (or a decreased in head) is accompanied by a reduction in inlet velocity 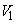 . But the flow velocity . But the flow velocity 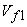 at inlet increases allowing a large amount of fluid to enter the turbine. The most important point to be noted in this context is that the flow at inlet to all the runners, except the Kaplan one, is in radial and tangential directions. Therefore, the inlet velocity triangles of those turbines (Figure 30.2a to 30.2d) are shown in a plane containing the radial ant tangential directions, and hence the flow velocity at inlet increases allowing a large amount of fluid to enter the turbine. The most important point to be noted in this context is that the flow at inlet to all the runners, except the Kaplan one, is in radial and tangential directions. Therefore, the inlet velocity triangles of those turbines (Figure 30.2a to 30.2d) are shown in a plane containing the radial ant tangential directions, and hence the flow velocity 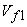 represents the radial component of velocity. represents the radial component of velocity.
In case of a Kaplan runner, the flow at inlet is in axial and tangential directions. Therefore, the inlet velocity triangle in this case (Figure 30.2e) is shown in a place containing the axial and tangential directions, and hence the flow velocity 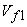 represents the axial component of velocity represents the axial component of velocity
 .The tangential component of velocity is almost nil at outlet of all runners. Therefore, the outlet velocity triangle (Figure 30.2f) is identical in shape of all runners. However, the exit velocity .The tangential component of velocity is almost nil at outlet of all runners. Therefore, the outlet velocity triangle (Figure 30.2f) is identical in shape of all runners. However, the exit velocity
 is axial in Kaplan and Dubs runner, while it is the radial one in all other runners. is axial in Kaplan and Dubs runner, while it is the radial one in all other runners.
| (a) Francis runner for low specific speeds |
(b) Francis runner for normal specific speeds |
(c) Francis runner for high specific speeds |
| (f) For allreaction (Francis as well as Kaplan) runners |
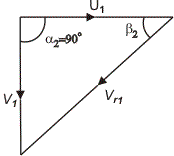 |
| Fig. 30.2 Evolution of Kaplan runner form Francis one |
|