Effect of Area Variation on Flow Properties in Isentropic Flow
In considering the effect of area variation on flow properties in isentropic flow, we shall concern ourselves primarily with the velocity and pressure. We shall determine the effect of change in area, A, on the velocity V, and the pressure p.
From Bernoulli's equation, we can write
or, 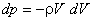 |
Dividing by 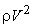 , we obtain , we obtain
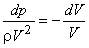 |
(19.1) |
A convenient differential form of the continuity equation can be obtained from Eq. (14.50) as
Substituting from Eq. (19.1),
Invoking the relation (
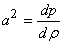 ) for isentropic process in Eq. (19.2), we get ) for isentropic process in Eq. (19.2), we get
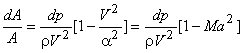 |
(19.3) |
From Eq. (19.3), we see that for Ma<1 an area change causes a pressure change of the same sign, i.e. positive dA means positive dp for Ma<1. For Ma>1, an area change causes a pressure change of opposite sign.
Again, substituting from Eq.(19.1) into Eq. (19.3), we obtain
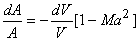 |
(19.4) |
From Eq. (19.4), we see that Ma<1 an area change causes a velocity change of opposite sign, i.e. positive dA means negative dV for Ma<1. For Ma>1, an area change causes a velocity change of same sign.
These results are summarized in Fig.19.1, and the relations (19.3) and (19.4) lead to the following important conclusions about compressible flows:
- At subsonic speeds (Ma<1) a decrease in area increases the speed of flow. A subsonic nozzle should have a convergent profile and a subsonic diffuser should possess a divergent profile. The flow behaviour in the regime of Ma<1 is therefore qualitatively the same as in incompressible flows.
- In supersonic flows (Ma>1), the effect of area changes are different. According to Eq. (19.4), a supersonic nozzle must be built with an increasing area in the flow direction. A supersonic diffuser must be a converging channel. Divergent nozzles are used to produce supersonic flow in missiles and launch vehicles.
| Fig 19.1 |
Shapes of nozzles and diffusersin subsonic and supersonic regimes |
Suppose a nozzle is used to obtain
a supersonic stream staring from low speeds at the
inlet (Fig.19.2). Then the Mach number should increase
from Ma=0 near the inlet to Ma>1 at the exit.
It is clear that the nozzle must converge in the
subsonic portion and diverge in the supersonic portion.
Such a nozzle is called a convergent-divergent
nozzle. A convergent-divergent nozzle is also
called a de Laval nozzle, after Carl G.P.
de Laval who first used such a configuration in his
steam turbines in late nineteenth century (this has
already been mentioned in the introductory note).
From Fig.19.2 it is clear that the Mach number must
be unity at the throat, where the area is neither
increasing nor decreasing. This is consistent with
Eq. (19.4) which shows that dV can
be non-zero at the throat only if Ma=1. It also follows
that the sonic velocity can be achieved only at the
throat of a nozzle or a diffuser.
|
Fig 19.2 A
convergent-divergent nozzle
|
The condition, however, does not
restrict that Ma must necessarily be unity
at the throat, According to Eq. (19.4), a situation
is possible where 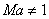 at
the throat if dV=0 there. For an example,
the flow in a convergent-divergent duct may be subsonic
everywhere with Ma increasing in the convergent
portion and decreasing in the divergent portion with at
the throat if dV=0 there. For an example,
the flow in a convergent-divergent duct may be subsonic
everywhere with Ma increasing in the convergent
portion and decreasing in the divergent portion with 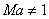 at
the throat (see Fig.19.3). The first part of the
duct is acting as a nozzle, whereas the second part
is acting as a diffuser. Alternatively, we may have
a convergent-divergent duct in which the flow is
supersonic everywhere with Ma decreasing
in the convergent part and increasing in the divergent
part and again at
the throat (see Fig.19.3). The first part of the
duct is acting as a nozzle, whereas the second part
is acting as a diffuser. Alternatively, we may have
a convergent-divergent duct in which the flow is
supersonic everywhere with Ma decreasing
in the convergent part and increasing in the divergent
part and again 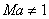 at
the throat (see Fig. 19.4). at
the throat (see Fig. 19.4).
|
Fig
19.3 Convergent-divergent
duct with 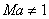 at
throat at
throat |
| Fig 19.4 |
Convergent-divergent
duct with 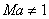 at
throat at
throat |
|