Iscentropic Flow of a vapor or gas
through a nozzle
First law of thermodynamics:
|
(if 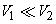 ) ) |
where 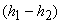 is enthalpy drop across the nozzle is enthalpy drop across the nozzle
Again we know, Tds = dh - νdp
For the isentropic flow, dh
= νdp
or, 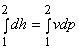 |
or, 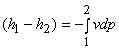 |
(20.1) |
Assuming
that the pressure and volume of steam during expansion
obey the law
pνn = constant, where n is the isentropic index
| |
|
| |
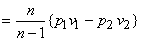 |
(20.2) |
Now, mass flow rate
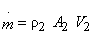
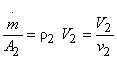
Therefore, the mass flow rate at the exit of the nozzle 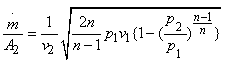
= 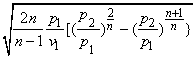 |
(20.3) |
The exit pressure,
p2 determines the  for
a given inlet condition. The mass flow rate is maximum
when, for
a given inlet condition. The mass flow rate is maximum
when,
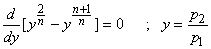
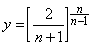
For maximum 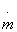 , ,
n = |
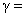 1.4, 1.4, |
for diatomic gases |
| |
|
for super
saturated steam |
| |
|
|
| |
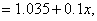 |
for wet steam
with dryness fraction x |
For , 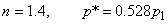 (50%drop in inlet pressure) (50%drop in inlet pressure)
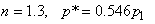
If we compare this with the results
of sonic properties, as described in the earlier
section, we shall observe that the critical pressure
occurs at the throat for Ma = 1. The critical pressure
ratio is defined as the ratio of pressure at the
throat to the inlet pressure, for checked flow when
Ma = 1
|