Nozzle, Steam Nozzle and Steam Turbine
STAGNATION, SONIC PROPERTIES AND ISENTROPIC EXPANSION IN NOZZLE
The stagnation values are useful reference conditions in a compressible flow. Suppose the properties of a flow (such as T, p, ρ etc.) are known at a point. The stagnation properties at a point are defined as those which are to be obtained if the local flow were imagined to cease to zero velocity isentropically. The stagnation values are denoted by a subscript zero. Thus, the stagnation enthalpy is defined as
For a calorically perfect gas, this yields,
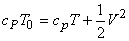 |
(18.1) |
which defines the stagnation temperature. It is meaningful to express the ratio of 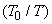 in the form in the form
or, 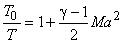 |
(18.2) |
If we know the local temperature (T) and Mach number (Ma), we can fine out the stagnation temperature 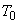 . Consequently, isentropic relations can be used to obtain stagnation pressure and stagnation density as. . Consequently, isentropic relations can be used to obtain stagnation pressure and stagnation density as.
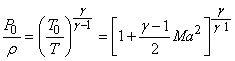 |
(18.3) |
In general, the stagnation properties can vary throughout the flow field.
However, if the flow is adiabatic,
then 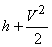 is
constant throughout the flow. It follows that the is
constant throughout the flow. It follows that the 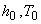 and and 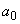 are
constant throughout an adiabatic flow, even in the
presence of friction. Here a is the speed of sound
and the suffix signifies the stagnation condition.
It is understood that all stagnation properties are
constant along an isentropic flow. If such a flow
starts from a large reservoir where the fluid is
practically at rest, then the properties in the reservoir
are equal to the stagnation properties everywhere
in the flow (Fig. 18.1). are
constant throughout an adiabatic flow, even in the
presence of friction. Here a is the speed of sound
and the suffix signifies the stagnation condition.
It is understood that all stagnation properties are
constant along an isentropic flow. If such a flow
starts from a large reservoir where the fluid is
practically at rest, then the properties in the reservoir
are equal to the stagnation properties everywhere
in the flow (Fig. 18.1).
| Fig 18.1 |
An isentropic process starting from a reservoir |
There is another set of conditions of comparable usefulness where the flow is sonic, Ma=1.0. These sonic, or critical properties are denoted by asterisks: 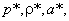 and. and. 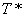 . These properties are attained if the local fluid is imagined to expand or compress isentropically until it reachers Ma=1. . These properties are attained if the local fluid is imagined to expand or compress isentropically until it reachers Ma=1.
We have already discussed that the total enthalpy, hence 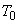 , is conserved so long the process is adiabatic, irrespective of frictional effects. In contrast, the stagnation pressure , is conserved so long the process is adiabatic, irrespective of frictional effects. In contrast, the stagnation pressure 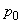 and density and density 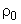 decrease if there is friction. decrease if there is friction. From Eq.(18.1), we note that
or, 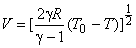 |
(18.5a) |
is the relationship between the fluid velocity and local temperature (T), in an adiabatic flow. The flow can attain a maximum velocity of
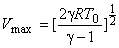 |
(18.5b) |
As it has already been stated, the unity Mach number, Ma=1, condition is of special significance in compressible flow, and we can now write from Eq.(18.2), (18.3) and (18.4).
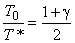 |
(18.6a) |
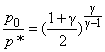 |
(18.6b) |
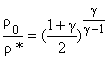 |
(18.6c) |
For diatomic gases, like air 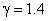 , the numerical values are , the numerical values are 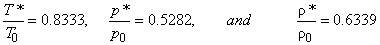
The fluid velocity and acoustic speed are equal at sonic condition and is
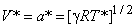 |
(18.7a) |
or, 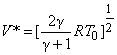 |
( 18.7b ) |
We shall employ both stagnation conditions and critical conditions as reference conditions in a variety of one dimensional compressible flows.
|