S,C -depend on the design of the cascade
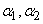 - flow angles at the inlet and outlet - flow angles at the inlet and outlet
Lift is perpendicular to 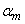 line line
Turbine Cascade: Static pressure will drop across the turbine cascade, i.e 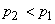
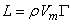
Lift coefficient, 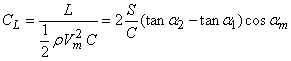
Above discussion is based on Kutta-Joukowski theorem
Assumption - Inviscid flow
In reality, we face viscous flow together with formation of wakes. Thus, the viscous flow is the cause of drag which in turn affect the lift .
Effect of viscous flow
As the fluid passes through the cascade, there will be a decrease in total pressure between the inlet to the cascade and at a section well downstream of the cascade due to frictional effect on aerofoils and also losses due to mixing of blade wades (i.e. the effect of viscous flow). Since at up and downstream, the flow is uniform and kinematics of flow remains unchanged, the dynamic pressure at up and downstream remains the same. Thus loss in total pressure is the same as that of static pressure.
The loss in total pressure 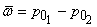 consists of two components: consists of two components:
(1) Frictional loss due to the formation of boundary layer on blades.
(2) Mixing of the blade wades.
.
Compressor Cascade (Viscous Case)
In compressor cascade, due to losses in total pressure 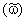 , there will be an axial force , there will be an axial force 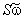 as shown in figure below. Thus the drag, which is perpendicular to the lift, is defined as as shown in figure below. Thus the drag, which is perpendicular to the lift, is defined as
The lift will be reduced due to the effect of drag which can be expressed as:
Effective lift = 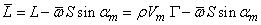
The lift has decreased due to viscosity,
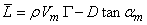
Actual lift coefficient 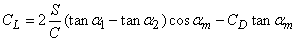
where, 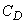 =drag coefficient, =drag coefficient, 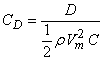
In the case of turbine, drag will contribute to work (and is considered as useful). |