Similarity
and Dimensional Analysis
Thus, 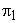 represents the condition for kinematic similarity, and is known as capacity coefficient or discharge coefficient The second represents the condition for kinematic similarity, and is known as capacity coefficient or discharge coefficient The second 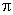 term term 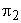 is known as the head coefficient since it expresses the head H in dimensionless form. Considering the fact that ND is known as the head coefficient since it expresses the head H in dimensionless form. Considering the fact that ND 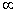 rotor velocity, the term rotor velocity, the term 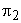 becomes becomes 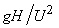 , and can be interpreted as the ratio of fluid head to kinetic energy of the rotor, Dividing , and can be interpreted as the ratio of fluid head to kinetic energy of the rotor, Dividing 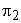 by the square of by the square of 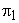 we get we get
The term 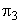 can be expressed as can be expressed as 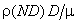 and thus represents the Reynolds number with rotor velocity as the characteristic velocity. Again, if we make the product of and thus represents the Reynolds number with rotor velocity as the characteristic velocity. Again, if we make the product of 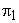 and and 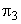 , it becomes , it becomes
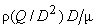 which represents the Reynolds's number based on fluid velocity. Therefore, if which represents the Reynolds's number based on fluid velocity. Therefore, if 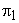 is kept same to obtain kinematic similarity, is kept same to obtain kinematic similarity, 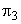 becomes proportional to the Reynolds number based on fluid velocity. becomes proportional to the Reynolds number based on fluid velocity.
The term 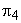 expresses the power P in dimensionless form and is therefore known as power coefficient . Combination of expresses the power P in dimensionless form and is therefore known as power coefficient . Combination of 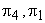 and and 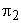 in the form of in the form of 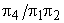 gives gives 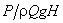 . The term 'PQgH' represents the rate of total energy given up by the fluid, in case of turbine, and gained by the fluid in case of pump or compressor. Since P is the power transferred to or from the rotor. Therefore . The term 'PQgH' represents the rate of total energy given up by the fluid, in case of turbine, and gained by the fluid in case of pump or compressor. Since P is the power transferred to or from the rotor. Therefore 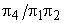 becomes the hydraulic efficiency becomes the hydraulic efficiency 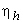 for a turbine and for a turbine and 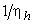 for a pump or a compressor. From the fifth for a pump or a compressor. From the fifth 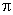 term, we get term, we get
Multiplying 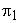 , on both sides, we get , on both sides, we get
Therefore, we find that 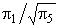 represents the well known Mach number , Ma. represents the well known Mach number , Ma.
For a fluid machine, handling incompressible fluid, the term 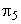 can be dropped. The effect of liquid viscosity on the performance of fluid machines is neglected or regarded as secondary, (which is often sufficiently true for certain cases or over a limited range).Therefore the term can be dropped. The effect of liquid viscosity on the performance of fluid machines is neglected or regarded as secondary, (which is often sufficiently true for certain cases or over a limited range).Therefore the term 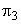 can also be dropped.The general relationship between the different dimensionless variables ( can also be dropped.The general relationship between the different dimensionless variables ( 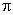 terms) can be expressed as terms) can be expressed as
Therefore one set of relationship or curves of the 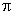 terms would be sufficient to describe the performance of all the members of one series. terms would be sufficient to describe the performance of all the members of one series.
|