Principle
of Similarity and Dimensional Analysis
The principle of similarity is a
consequence of nature for any physical phenomenon.
By making use of this principle, it becomes possible
to predict the performance of one machine from the
results of tests on a geometrically similar machine,
and also to predict the performance of the same machine
under conditions different from the test conditions.
For fluid machine, geometrical similarity must apply
to all significant parts of the system viz., the
rotor, the entrance and discharge passages and so
on. Machines which are geometrically similar form
a homologous series. Therefore, the member of such
a series, having a common shape are simply enlargements
or reductions of each other. If two machines are
kinematically similar, the velocity vector diagrams
at inlet and outlet of the rotor of one machine must
be similar to those of the other. Geometrical similarity
of the inlet and outlet velocity diagrams is, therefore,
a necessary condition for dynamic similarity.
Let us now apply dimensional analysis
to determine the dimensionless parameters, i.e.,
the π terms as the criteria of similarity for flows through fluid machines. For
a machine of a given shape, and handling compressible
fluid, the relevant variables are given in Table
3.1
Table 3.1
Variable Physical Parameters of Fluid Machine
Variable physical parameters |
Dimensional formula |
| |
|
D = any physical dimension of the machine as a measure of the machine's size, usually the rotor diameter |
|
Q = volume flow rate through the machine
|
L3 T -1
|
| N = rotational speed (rev/min.) |
|
H = difference in head (energy per unit weight) across the machine. This may be either gained or given by the fluid depending upon whether the machine is a pump or a turbine respectively
|
|
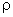 = density of fluid |
|
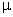 = viscosity of fluid = viscosity of fluid |
ML-1 T -1
|
| E = coefficient of elasticity of fluid |
ML-1 T-2
|
| g = acceleration due to gravity |
LT -2
|
P = power transferred between fluid and rotor (the difference between P and H is taken care of by the hydraulic efficiency 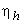 |
ML2 T-3
|
In almost all fluid machines flow with
a free surface does not occur, and the effect of gravitational
force is negligible. Therefore, it is more logical
to consider the energy per unit mass gH as
the variable rather than H alone so that
acceleration due to gravity does not appear as a separate
variable. Therefore, the number of separate variables
becomes eight: D, Q, N, gH, ρ, µ, E and P .
Since the number of fundamental dimensions required
to express these variable are three, the number of
independent π terms
(dimensionless terms), becomes five. Using Buckingham's π theorem
with D, N and ρ as the repeating variables,
the expression for the terms are obtained as,
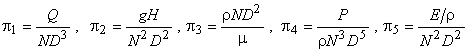 |
We
shall now discuss the physical significance and usual
terminologies of the different π terms. All lengths
of the machine are proportional to D ,
and all areas to D2. Therefore, the average
flow velocity at any section in the machine is proportional
to 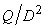 .
Again, the peripheral velocity of the rotor is proportional
to the product ND . The first π term
can be expressed as .
Again, the peripheral velocity of the rotor is proportional
to the product ND . The first π term
can be expressed as
|