Some Properties of the Finite Element Solution
Using the expressions for the linear, bilinear and quadratic forms (equations 2.45-2.47) and the idea of the strain energy of a bar, some properties of the finite element (FE) solution, especially those related to its convergence to the exact solution can be studied.
Let u be the exact solution of equations (2.1a-2.1c) and let 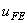 be the solution obtained by the finite element method. The error e between the solutions is defined as : be the solution obtained by the finite element method. The error e between the solutions is defined as :
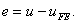 |
(9.17) |
Note that the integral form of the weighted residual method (equation 2.5b or 3.68) can be written in terms of the bilinear and linear forms using equations (2.45-2. 46).
Thus, we get
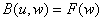 |
(9.18) |
However, while solving this equation, we use the approximation uFE . Therefore, we obtain
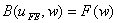 |
(9.19) |
Subtracting equation (9.19) from (9.18), we get
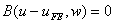 . . |
(9.20) |
Now, choose 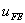 as the weight function w . Thus, as the weight function w . Thus,
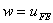 |
(9.21) |
Then, equation (9.20) can be written as :
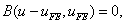 |
(9.22a) |
or
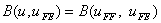 |
(9.22b) |
Using the definition of the error e (equation 9.17), equation (9.22a) becomes:
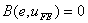 |
(9.23) |
Further, using the definition of the bilinear form B (equation 2.46), equation (9.23) can be expressed as:
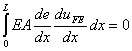 |
(9.24) |
Note that the strain energy U of a bar corresponding to the displacement field 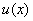 is given by is given by
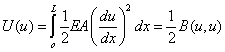 |
(9.25) |
Here, the expression (2.47) for the quadratic form is used. Then, using the definition of the error e (equation 9.17), we get the following expression for the strain energy associated with the error.
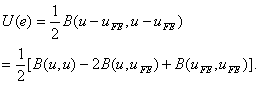 |
(9.26) |
Here, the symmetry of the bilinear form B with respect to its two arguments is used. Using equation (9.22b), we get
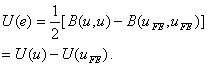 |
(9.27) |
Since,
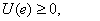 |
(9.28) |
we obtain
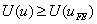 |
(9.29) |
Equation (9.29) states that the strain energy of the FE solution is always less than the strain energy of the exact solution. It means the finite element model of the bar is always stiffer than the actual bar. Equation (9.29) also means that, if we use the energy norm (given by equation 9.25) for studying the convergence , then the FE solution converges to the exact solution from below . It can be shown that the convergence is monotonic .
|