Application of Displacement (or Dirichlet) Boundary Condition
For piece-wise linear Lagrangian shape functions 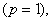 Lecture 7 discusses the algorithm of applying the displacement (or Dirichlet) boundary condition at the end Lecture 7 discusses the algorithm of applying the displacement (or Dirichlet) boundary condition at the end 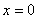 , i.e., at the first node , i.e., at the first node 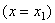 . This algorithm does not depend on the order p of the approximation. Instead, it depends on the number of degrees of freedom per node. Since, we are still using the Lagrangian approximation, the number of degrees of freedom per node remains the same. Therefore the algorithm of section 7.1 of applying the displacement (or Dirichlet) boundary condition remains valid even for higher order . This algorithm does not depend on the order p of the approximation. Instead, it depends on the number of degrees of freedom per node. Since, we are still using the Lagrangian approximation, the number of degrees of freedom per node remains the same. Therefore the algorithm of section 7.1 of applying the displacement (or Dirichlet) boundary condition remains valid even for higher order 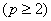 Lagrangian approximations. This algorithm, as given by equations (7.14-7.15), can be written as : Lagrangian approximations. This algorithm, as given by equations (7.14-7.15), can be written as :
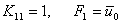 |
|
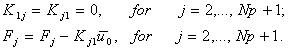 |
(9.16) |
Here, 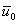 is the value of the displacement at the end x = 0, i.e. at the first node. is the value of the displacement at the end x = 0, i.e. at the first node.
Algorithm for solving the modified equations will be discussed in a separate Lecture.
|