| |
Assembly of Global Stiffness Matrix and Global Force Vector
For piecewise linear Lagrangian shape functions ( p = 1), the algorithm for the assembly procedure has been described in section 6.4. The algorithm does not depend on the order ( p ) of the approximation. Instead, it depends on the number of degrees of freedom per node. Since, we are still using the Lagrangian approximation; the number of degrees of freedom per node remains the same. Therefore, the assembly algorithm of section 6.4 remains valid even for higher order 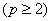 Lagrangian approximations. This algorithm is as follows. Lagrangian approximations. This algorithm is as follows.
First Step :
For each element, the element stiffness matrix 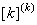 and the elements force vector and the elements force vector 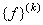 are expanded to the full size. This is done using equations (6.36)-(6.37). These equations can be written again as : are expanded to the full size. This is done using equations (6.36)-(6.37). These equations can be written again as :
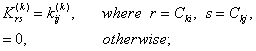 |
(9.10) |
and
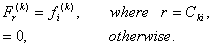 |
(9.11) |
Here [ C ] is the connectively matrix. The number of rows in the connectivity matrix is equal to the number of elements N . The number of columns in the connectivity matrix is equal to the number of nodes per element. Thus, for piecewise linear (Lagrangian) approximation 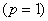 , the number of nodes per element is two. For piecewise quadratic (Lagrangian) approximation , the number of nodes per element is two. For piecewise quadratic (Lagrangian) approximation 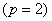 , the number of nodes per element is three. For pth order (Lagrangian) approximation, the number of nodes per element is p +1. Therefore, the corresponding number of columns in [ C ] is ( p +1). Note that, a typical component , the number of nodes per element is three. For pth order (Lagrangian) approximation, the number of nodes per element is p +1. Therefore, the corresponding number of columns in [ C ] is ( p +1). Note that, a typical component 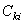 of [C] represents the global number of the local node i belonging to the element k . Thus, from Figures 9.1 and 9.2, we can write the algorithm for generating [ C ] as follows : of [C] represents the global number of the local node i belonging to the element k . Thus, from Figures 9.1 and 9.2, we can write the algorithm for generating [ C ] as follows :
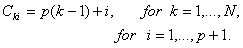 |
(9.12) |
Second Step :
In the 2 nd step, we add the expanded matrices [ K ] (k) and the expanded vectors 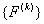 to obtain the global stiffness matrix [ K ] and the global force vector { F }. Further, at this stage, the point force P at the last node (i.e., at the point to obtain the global stiffness matrix [ K ] and the global force vector { F }. Further, at this stage, the point force P at the last node (i.e., at the point  ) is also added to the last column of { F }. This is how the Neumann boundary condition at the end ) is also added to the last column of { F }. This is how the Neumann boundary condition at the end 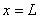 (equation 2.1c) is taken care of. Thus, the algorithm for the second step is written as (equations 6.38-6.39) : (equation 2.1c) is taken care of. Thus, the algorithm for the second step is written as (equations 6.38-6.39) :
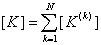 , , |
(9.13) |
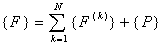 |
(9.14) |
The vector {P} for the case of p = 1 is given by equation (6.41). For general p , it is given by
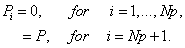 |
(9.15) |
|