| |
Calculation of Element Stiffness Matrix and Element Force Vector
When pth order approximation is used, there are ( p +1) nodes per element. Further, there is only 1 degree of freedom (dof) per node. Thus, there are ( p +1) dof per element. As a result, the size of the element shiftiness matrix 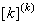 is is 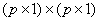 while that of the element force vector while that of the element force vector 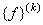 is is 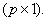 For p = 1 (i.e., the 1st order approximation with piecewise linear shape functions), the sizes of For p = 1 (i.e., the 1st order approximation with piecewise linear shape functions), the sizes of 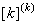 and and 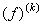 are are 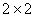 and 2 respectively. The corresponding expressions are given by equations (6.25-6.26). For p = 2 (i.e., the 2 nd order approximation with piecewise quadratic shape functions), the sizes of and 2 respectively. The corresponding expressions are given by equations (6.25-6.26). For p = 2 (i.e., the 2 nd order approximation with piecewise quadratic shape functions), the sizes of 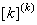 and and 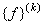 are are 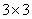 and 3 respectively. The corresponding expressions are given by equations (8.30-8.31). Generalizing these equations for and 3 respectively. The corresponding expressions are given by equations (8.30-8.31). Generalizing these equations for 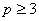 , and writing them in the index notation, we get the following expressions for the elements stiffness matrix , and writing them in the index notation, we get the following expressions for the elements stiffness matrix 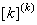 and the element force vector and the element force vector 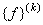 : :
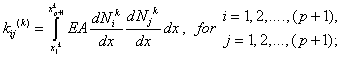 |
(9.8) |
and
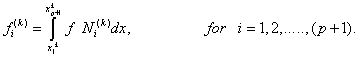 |
(9.9) |
The area of cross-section ( A ) of the bar, the Young's modulus ( E ) of the bar material and the distributed force ( f ) acting on the bar are given as functions of x . Further, the shape functions 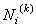 are given by the expression (9.6). Using all this information, the element stiffness matrix are given by the expression (9.6). Using all this information, the element stiffness matrix 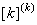 and the element stiffness vector and the element stiffness vector 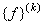 are calculated using the expressions (9.8-9.9). This is done for all the elements. are calculated using the expressions (9.8-9.9). This is done for all the elements.
|