Mesh and Shape Functions

We divide the domain (i.e., the interval of length L ) into N elements. We assume that the mesh is uniform. Then, the element length is given by

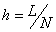(9.1)

If we use p^th order basis functions to approximate the primary variable, then the number of nodes per element is p +1. Further, the total number of nodes in the domain is

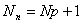(9.2)

Figure 9.1 shows a typical mesh with the element numbering system, the global node numbering system and the global notation for the co-ordinates and the degrees of freedom (dof). The co-ordinates can be written as :

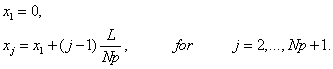(9.3)

Figure 9.1 Typical mesh with p^th order approximation

A typical element k with the local node numbering system and the local notation for the coordinates and the degrees of freedom is shown in Fig. 9.2.

Figure 9.2 Typical element k

As stated earlier, when we use p th order approximation, there are Np +1 global nodes. Thus, there are Np +1 global basis functions. Further, there are ( p +1) nodes per element. Thus, there are ( p +1) shape functions. The procedures of obtaining the shape functions for the case of p = 1 and 2 have been explained in Lectures 6 and 8 respectively. These expressions are given by equations (6.1-6.2) and (8.6) :

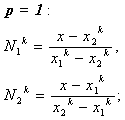(9.4)

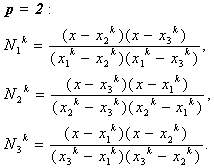(9.5)

Using the method of mathematical induction, we get the following expressions for the shape functions for p^th order approximation :

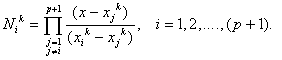(9.6)

For p = 1, 2 and 3, these shape functions are shown in Fig. 9.3

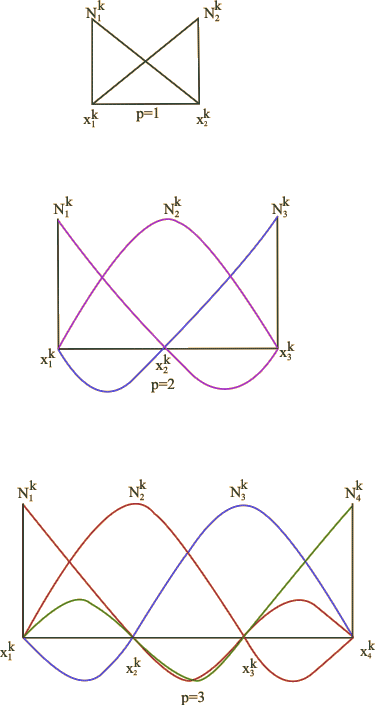
Figure 9.3 Linear ( p = 1), quadratic ( p = 2) and cubic ( p = 3) shape functions

When only the primary variable is used as the dof, the shape functions (equation 9.6) which we get are the same as the Lagrangian interpolation functions. Therefore, these shape functions are called as Lagrangian shape functions . Equation (9.6) represents the Lagrangian family of shape functions for p = 1, 2,... The corresponding element is called as the Lagrangian element . From equation (9.6) and Fig. 9.3, We can deduce the following properties of the shape functions :

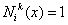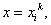
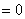• at node i , i.e., at
   at node j , i.e., at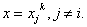

Thus,

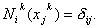(9.7)

• There are ( p -1) internal or bubble shape functions which are non-zero only in the interior of the element and are zero outside the element, i.e., outside the interval
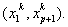