Convergence of Finite Element Solution
Convergence of the finite element solution to the exact solution will be considered in the next lecture. Here, we state some properties of the convergence without proof.
- Convergence of the Nodal Values :
When EA = constant, the values at the end-points of the element 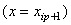 match with the exact values. That is match with the exact values. That is
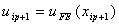 |
for i = 1,2,.. |
(9.30) |
For all other cases ( EA 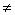 constant), constant), 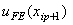 is close to the exact value is close to the exact value 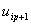 . .
- Convergence of the Derivatives :
To discuss the convergence of the derivatives, consider a simple example, where AE=1, L=1, f=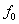 =1, P = 10. Then, equations (2.1a - 2.1c) become : =1, P = 10. Then, equations (2.1a - 2.1c) become :
D.E. : 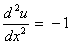 , , |
0 < x <1; |
(9.31a) |
| B.C. : (i) u = 0, |
at x = 0, |
(9.31b) |
(ii) 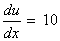 , , |
at x = 1. |
(9.31c) |
If is easy to see that the exact solution of this problem is
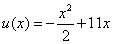 |
(9.32) |
Then, the derivative of the exact solution is
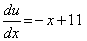 |
(9.33) |
Suppose we use a linear approximation to solve this problem, then, over a typical element k, the FE approximation is (equation 6.5) :
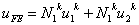 |
(9.34) |
where the expressions for the shape functions are (equations 6.30-6.31) :
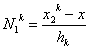 , |
(9.35) |
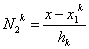 |
(9.36) |
Here, the element length hk is given by
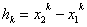 |
(9.37) |
The element stiffness matrix [ k ] e and the element force vector { f } e , then, are given by equations (6.32-6.33). Using AE = 1, f0 = 1 we get
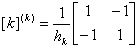 , , |
(9.38) |
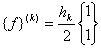 |
(9.39) |
Suppose we use a mesh of 3 elements ( N = 3) and 4 nodes. Further, we assume that the mesh is uniform. Then, for each element, we have
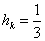 |
(9.40) |
This mesh is shown in Fig. 9.4 and a typical element k is shown in Fig. 9.5.

Figure 9.4 Three element uniform mesh
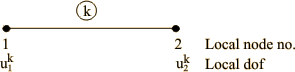
Figure 9.5 Typical element k
For this mesh, the connectivity matrix [C] relating the local and global node numbering system is given by
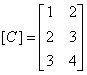 |
(9.41) |
Using equations (6.36-6.41) for assembling the global stiffness matrix [ K ] and the global force vector { F }, we get the following expressions. Note that, the value of P is 10.
 , , |
(9.42) |
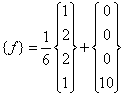 |
(9.43) |
The finite element equations become:
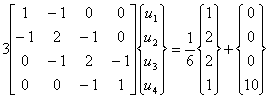 |
(9.44) |
The boundary condition (9.31b) means
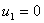 |
(9.45) |
Using the procedure of section 7.1 for applying this boundary condition, we get the following modified equation :
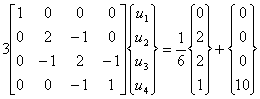 |
(9.46) |
The solution of the modified system of algebraic equations is
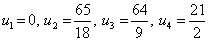 |
(9.47) |
To find the derivative of the FE solution, we substitute the expressions (9.35 - 9.36) for the shape functions N i k in the FE approximation (9.34) and then differentiate. For a typical element k , we get
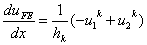 . . |
(9.48) |
Using the values of hk from equation (9.40), we obtain
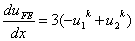 |
(9.49) |
For the first element ( k = 1) :
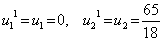 . . |
(9.50) |
Therefore,
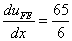 , (1st element). , (1st element). |
(9.51) |
Similarly, for the second element ( k = 2) :
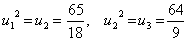 . . |
(9.52) |
Therefore,
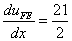 , (2nd element). , (2nd element). |
(9.53) |
Finally, for the third element ( k = 3) :
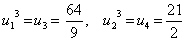 |
(9.54) |
Therefore,
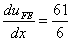 , (3rd element). , (3rd element). |
(9.55) |
The variations of the derivative of the exact solution 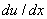 (equation 9.33) and the derivative of FE solution (equation 9.33) and the derivative of FE solution 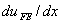 (equations 9.51, 9.53 and 9.55) are plotted in Fig. 9.6. (equations 9.51, 9.53 and 9.55) are plotted in Fig. 9.6.
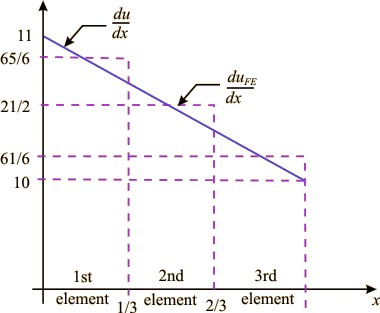
Figure 9.6 Variations of the derivatives of the exact and FE solutions.
The figure shows that, when the FE approximation for the primary variable is piecewise linear, the derivative of the FE solution is discontinuous at the nodes and constant over each element. Further, the values of 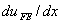 match with the values of the match with the values of the 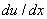 at the centre point of each element. Thus, for linear approximation at the centre point of each element. Thus, for linear approximation
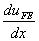 = = 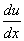 , at the centre of each element. , at the centre of each element. |
(9.56) |
This is called super convergence .
|