| |
Approximation for the Primary Variable using Piecewise Quadratic Basis Functions
For the purpose of deriving the finite element equations, we approximate the primary variable u(x) as follows:
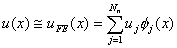 |
|
(8.9) |
Here, 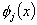 are the piecewise quadratic basis functions and N n is the number of nodes of the domain. When the piecewise linear basis functions are used, the number of nodes of the domain ( N n ) is equal to the number of elements ( N ) plus one. For the case of piecewise quadratic basis functions, Nn = 2N +1. Thus, for 4-element mesh of Fig. 8.3, Nn is 9. Here, the unknown coefficients are the piecewise quadratic basis functions and N n is the number of nodes of the domain. When the piecewise linear basis functions are used, the number of nodes of the domain ( N n ) is equal to the number of elements ( N ) plus one. For the case of piecewise quadratic basis functions, Nn = 2N +1. Thus, for 4-element mesh of Fig. 8.3, Nn is 9. Here, the unknown coefficients 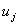 have the following interpretation. At node have the following interpretation. At node 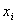 , we have , we have
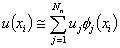 |
(8.10) |
Using equation (8.1), we get
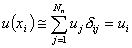 |
(8.11) |
Thus, 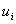 is the value of the primary variable at node ' i '. This is the characteristics of the Lagrangian interpolation functions. As stated in section 6.1, the values is the value of the primary variable at node ' i '. This is the characteristics of the Lagrangian interpolation functions. As stated in section 6.1, the values 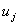 , j = 1, 2., , j = 1, 2.,  are called the degrees of freedom (abbreviated as dof ). are called the degrees of freedom (abbreviated as dof ).
In section 8.1, we stated some properties of the basis functions 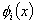 . Now we shall discuss some additional properties. For this purpose, let us differentiate equation 8.9. Then, we get . Now we shall discuss some additional properties. For this purpose, let us differentiate equation 8.9. Then, we get
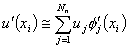 |
(8.12) |
Further, assume that the primary variable u ( x ) is a constant function with the value unity. Thus
| u ( x ) = 1, |
for x 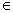 (0, L ). (0, L ). |
(8.13) |
Then
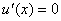 |
for x 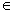 (0, L ). (0, L ). |
(8.14) |
Note that, for such a function, the nodal value of u(x) is unity at all the nodes. Thus,
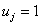 |
for j = 1,2 ., 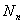 . . |
(8.15) |
Substituting equations (8.13 - 8.15) in equations (8.9) and (8.12) we get
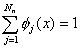 , , |
(8.16a) |
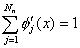 |
(8.16b) |
When ' j ' is even, the basis function 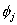 is completely defined over the element j /2. It is a bubble function as shown in Fig. 8.3. Note that, its derivative is not continuous at the end points is completely defined over the element j /2. It is a bubble function as shown in Fig. 8.3. Note that, its derivative is not continuous at the end points 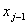 and and 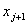 or at the nodes j -1 and j +1. When ' j ' is odd, the basis function is defined over the 2 elements ( j +1)/2 and [(( j +1)/2)-1]. Thus, it shares a common node 'j' of these 2 elements. The derivative of this function is discontinuous at the end nodes ( j -2) and ( j +2) as well as the common node 'j'. Thus, u is discontinuous at the points or at the nodes j -1 and j +1. When ' j ' is odd, the basis function is defined over the 2 elements ( j +1)/2 and [(( j +1)/2)-1]. Thus, it shares a common node 'j' of these 2 elements. The derivative of this function is discontinuous at the end nodes ( j -2) and ( j +2) as well as the common node 'j'. Thus, u is discontinuous at the points 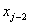 , , 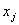 and and 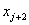 . The functions . The functions 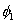 and and 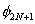 are defined over only 1 element, namely 1 st and N th . Therefore, they are discontinuous only at the end points of these elements. Unlike the properties given by equations (8.16 - 8.17), the last property will be different when ' p ' is different. are defined over only 1 element, namely 1 st and N th . Therefore, they are discontinuous only at the end points of these elements. Unlike the properties given by equations (8.16 - 8.17), the last property will be different when ' p ' is different.
For kth element, the only non-zero basis functions are 2k -1, 2k and 2k +1 (see Fig. 8.3). Thus, the approximation (8.9) for the element ' k ' becomes
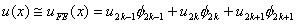 |
(8.17) |
Note that the local notation for 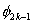 , , 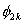 and and 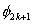 is is 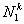 , , 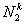 and and 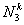 respectively. For the convenience of the element wise evaluation of the stiffness matrix and force vector, we introduce a local notation for the degrees of freedom respectively. For the convenience of the element wise evaluation of the stiffness matrix and force vector, we introduce a local notation for the degrees of freedom 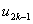 , , 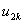 and and 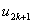 . In the local notation, we call them as . In the local notation, we call them as 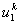 , , 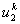 and and 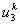 . Then, the expression (8.17), in local notation becomes . Then, the expression (8.17), in local notation becomes
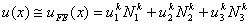 |
(8.18) |
|