Piecewise Basis Functions of Order Higher than Two

Following the procedure of section 8.1, we can construct the piece-wise basis functions of order higher than two. Thus, we can construct piecewise cubic, piecewise quartic, piecewise quintic basis functions etc. At the element level, the expressions for the basis functions (called as the shape or interpolation functions) are given by

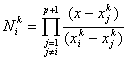for i = 1,2,3.., p +1 .

(8.8)

where 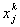is the local notation for the coordinate and ' p ' is the order of the basis functions.

Equation (8.8) is the expression for the Lagrangian shape or interpolation function of the order ' p '. Note that for p = 1, this expression reduces to equations (6.1-6.2) for the piecewise linear basis functions (called as the Lagrangian shape or interpolation functions of order 1). Further, for p = 2, this expression reduces to equation (8.7) for the piecewise quadratic basis functions (called as the Lagrangian shape or interpolation functions of order 2).