| |
Piecewise Quadratic Basis Functions
Figure 8.3 shows the piecewise quadratic basis functions 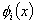 for a 4-element mesh. Note that, now, there are 2 nodes per element or totally 9 nodes. Further, the figure also shows the element numbering system and the global notation for the nodes and coordinates. for a 4-element mesh. Note that, now, there are 2 nodes per element or totally 9 nodes. Further, the figure also shows the element numbering system and the global notation for the nodes and coordinates.
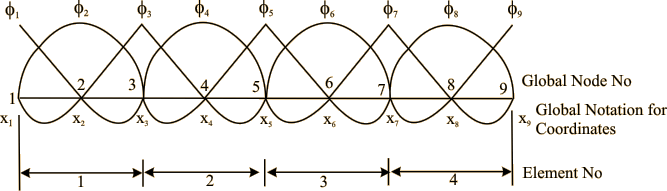
Figure 8.3: Piece wise quadratic basis functions for 4 - element mesh
To generate these shape functions, we note that, like the piecewise linear basis functions of Fig. 4.3, these functions should satisfy the following requirements:
- Each function
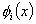 must be 1 at node 'i' and vanish at all other nodes. Thus, must be 1 at node 'i' and vanish at all other nodes. Thus,
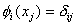 |
(8.1) |
- Each function must have a local (or compact) support. Thus, each
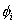 must vanish outside a certain interval of the domain. must vanish outside a certain interval of the domain.
- The set of
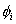 must be linearly independent. That is, the solution of the equation involving scalar coefficients must be linearly independent. That is, the solution of the equation involving scalar coefficients 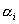
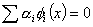 |
for x 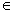 [0, L ] [0, L ] |
(8.2) |
must imply that
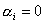 |
for all i . |
(8.3) |
But, like the functions of Fig.4.3, the variation of these functions is not linear. Instead,
- Each function
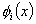 has quadratic variation with 'x'. has quadratic variation with 'x'.
To generate the mathematical expression for these functions, we proceed as follows. We consider a typical element 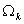 and the three basis functions which are non-zero over this element. This is shown in Fig. 8.4 and the three basis functions which are non-zero over this element. This is shown in Fig. 8.4
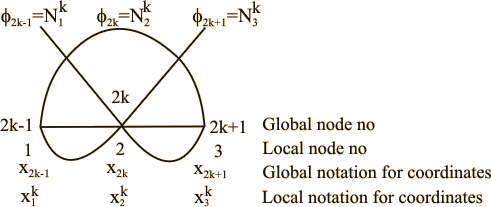
Figure 8.4: Typical element k, the non-zero basis functions and
the local notation for the nodes, coordinates and basis functions
Note that, the basis functions which are non-zero on the element 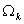 are are 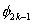 , , 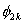 and and 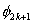 . For the convenience of the element wise evaluation of the stiffness matrix and the force vector, at the element level, we introduce a local notation for these basis functions. In the local notation, we call them as . For the convenience of the element wise evaluation of the stiffness matrix and the force vector, at the element level, we introduce a local notation for these basis functions. In the local notation, we call them as 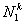 , , 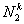 and and 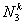 . Similarly we introduce a local notation for the nodal coordinates images . Similarly we introduce a local notation for the nodal coordinates images 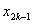 , , 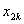 and and 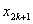 of the element of the element 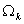 . In the local notation, we call them as . In the local notation, we call them as 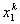 , , 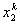 and and 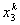 . Further, for the nodes 2k-1, 2k and 2k+1 of the element . Further, for the nodes 2k-1, 2k and 2k+1 of the element 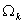 , we introduce a local numbering system. Now, we number these nodes as 1, 2 and 3. The local notation for the basis functions, the coordinates and the nodes is shown in Fig. 8.4. , we introduce a local numbering system. Now, we number these nodes as 1, 2 and 3. The local notation for the basis functions, the coordinates and the nodes is shown in Fig. 8.4.
Since each basis function is a quadratic function of 'x', we can write it as
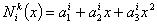 , , |
for i = 1,2,3. |
(8.4) |
The unknown constants 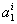 , , 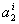 and and 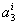 can be determined from the following condition. Note that at node 'j', that is at can be determined from the following condition. Note that at node 'j', that is at 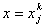 , the value of the function , the value of the function 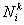 is '1' if i = j and '0' if i ? j .Thus, is '1' if i = j and '0' if i ? j .Thus,
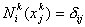 |
(8.5) |
Evaluating equation (8.4) at 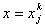 and then substituting in equation (8.5), we get 3 equations for 3 unknowns and then substituting in equation (8.5), we get 3 equations for 3 unknowns 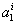 , , 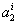 and and 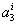 . By solving these equations for . By solving these equations for 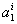 , , 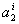 and and 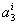 and substituting these expressions in equation (8.4), we get the basis functions and substituting these expressions in equation (8.4), we get the basis functions 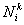 in terms of the coordinates in terms of the coordinates 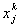 . We do these for each 'i'. The expressions for the basis functions are: . We do these for each 'i'. The expressions for the basis functions are:
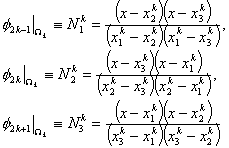 |
(8.6) |
The above equations can also be written as
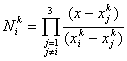 |
for i =1,2,3. |
(8.7) |
At the element level, these basis functions are called as the Lagrangian shape or interpolation functions .
|