Introduction

So far, we have used piecewise linear basis functions to approximate the primary variable. But in some problems, it may not approximate the solution properly unless we use a large number of elements. As an example, consider the problem of Fig. 8.1.

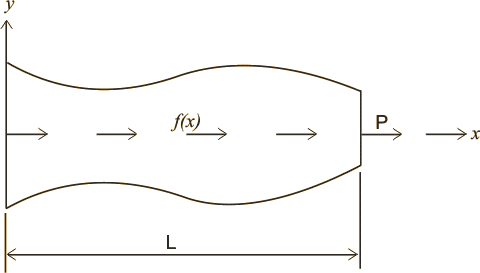
Figure 8.1

The bar of Fig.8.1 has a variable area of cross-section A ( x ). Further, the variation of the distributed force f ( x ) is not polynomial in nature. In this case, the variation of the solution u ( x ) with ' x ' is not polynomial as shown in Fig.8.2.

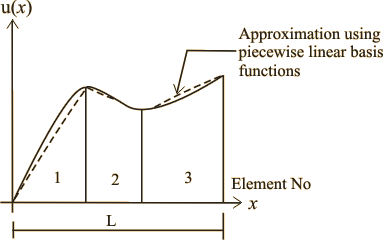
Figure 8.2

Figure 8.2 also shows the approximation of the solution using piecewise linear basis functions with three element mesh. It is quite clear that, if we use only the linear basis functions, many elements would be needed to have a better approximation. On the other hand, if we choose higher order (like quadratic, cubic etc.) basis functions, then only a few elements would be required. Next section discusses piecewise quadratic basis functions.