Natural Boundary Conditions at Both the Ends
Suppose, we have a bar where there is a natural or free boundary condition at both the ends
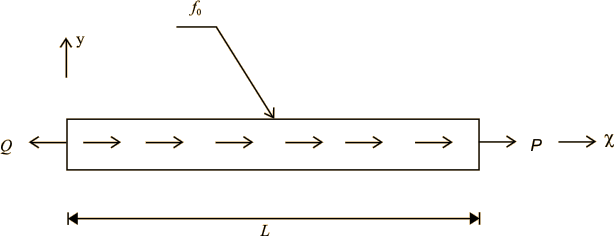
Figure 7.4 Bar with natural boundary conditions at both the ends
Then, for static equilibrium
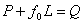 |
(7.27) |
Since, we have a force boundary condition at the left end also, the boundary condition (1.1b) gets modified to
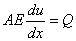 at x = 0. at x = 0. |
(7.28) |
Then, the weighted residual integral becomes
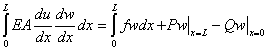 |
(7.29) |
If we develop the finite element equation for this problem using the 6-element mesh of Fig. 7.1, then the global stiffness matrix remains unchanged, but the global force vector become
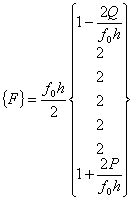 |
(7.30) |
Now the finite element equations become
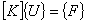 |
(7.31) |
or
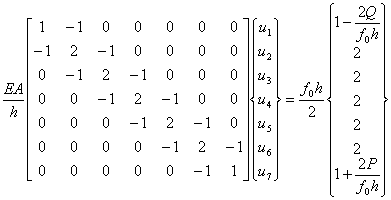 |
(7.32) |
Note that by adding all the equations, we get
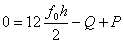 |
(7.33) |
Since 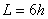 , we get , we get
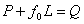 |
(7.34) |
This is the same equation as equation (7.27).
Note that, there are no essential boundary conditions. Therefore, no modification of either the stiffness matrix or the force vector is needed before we solve the system of equations (7.31). But there is a difficulty in solving these equations. It can be easily verified that the determinant of the stiffness matrix 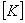 is zero or is zero or 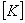 is singular . In this case, the system of equations (7.31) possesses many solutions or the solution is not unique . This can be seen as follows. Consider the vector is singular . In this case, the system of equations (7.31) possesses many solutions or the solution is not unique . This can be seen as follows. Consider the vector
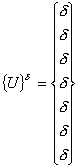 , ( , ( 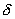 = arbitrary number). = arbitrary number). |
(7.35) |
It means all the nodal values of the axial displacement 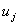 are identical (and are equal to are identical (and are equal to 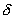 ). Then, equation (7.10) becomes ). Then, equation (7.10) becomes
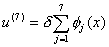 . . |
(7.36) |
This implies that the axial displacement of the rod is same at every point (and is equal to 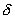 ). This represents the rigid translation of the bar. Note that ). This represents the rigid translation of the bar. Note that
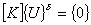 . . |
(7.37) |
Let 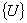 be a solution of the system of equations (7.31).Then be a solution of the system of equations (7.31).Then
Thus, if 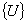 is a solution of the system of equations (7.31), then is a solution of the system of equations (7.31), then 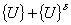 is also a solution of the same system of equations. Therefore, solution of the system of equations (7.31) is not unique. is also a solution of the same system of equations. Therefore, solution of the system of equations (7.31) is not unique.
To make the solution unique, we have to make sure that there is no vector like 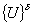 which satisfies the equation (7.37). In other words, we have to ensure that there is no rigid body translation mode in the deformation of the bar. To ensure this, we can set any nodal displacement which satisfies the equation (7.37). In other words, we have to ensure that there is no rigid body translation mode in the deformation of the bar. To ensure this, we can set any nodal displacement 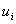 to any arbitrary value to any arbitrary value 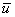 . To apply this condition, we carry out the modifications similar to equations (7.14) and (7.15): . To apply this condition, we carry out the modifications similar to equations (7.14) and (7.15):
- Replace the ith equation by the condition
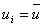 . Thus . Thus
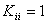 , , |
|
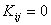 for j = 1,...,7, j for j = 1,...,7, j 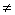 i , i , |
|
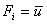 ; ; |
(7.39) |
- Transpose the known terms from the remaining equations to the right side :
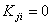 |
for j = 1,...,7, j 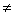 i, i, |
|
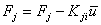 |
for j = 1,...,7, j 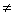 i i |
(7.40) |
Then, the modified 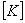 becomes non singular and we can solve the modified system of equations to get a unique solution. Note that the solution gives becomes non singular and we can solve the modified system of equations to get a unique solution. Note that the solution gives 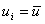 . .
|