| |
Essential Boundary Conditions at Both the Ends
Consider a bar whose both ends are fixed as shown in Fig. 7.3.
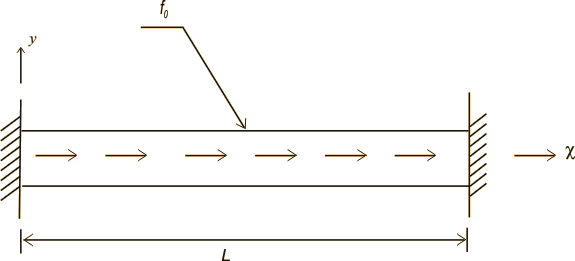
Figure 7.3 Bar with essential boundary condition at both the ends
Since, we have an essential boundary condition at the end 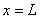 also, the boundary conditions (1.1c) becomes also, the boundary conditions (1.1c) becomes
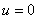 at at 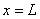 . . |
(7.18) |
Then the weighted residual expression becomes
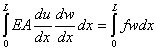 |
(7.19) |
If we develop the finite element equations for this problem using the 6-element mesh of Fig. 7.1, then the global stiffness matrix remains unchanged, but the global force vector becomes
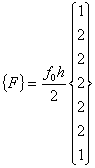 |
(7.20) |
Now the finite element equations become
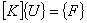 |
(7.21) |
or
 . . |
(7.22) |
The essential boundary condition at the left end ( x = 0)
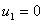 |
(7.23) |
is applied by modifying the matrix 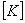 and the vector and the vector 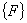 using the expressions (7.14) and (7.15). Note that, here using the expressions (7.14) and (7.15). Note that, here 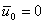 . The essential boundary condition at the right end ( . The essential boundary condition at the right end ( 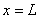 ) )
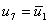 , , 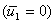 |
(7.24) |
is also applied in similar fashion. But now, it is the nodal displacement of the 7th node that is known. Therefore, we apply the boundary condition as follows :
- Replace the 7th equation by the condition
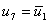 . Thus . Thus
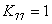 , , |
|
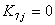 |
for j = 1,..,6, |
|
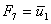 ; ; |
(7.25) |
- Transpose the known terms from the first 6 equations to the right side :
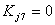 |
for j = 1,..,6, |
|
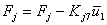 |
for j = 1,.., 6. |
(7.26) |
|