| |
Application of the Standard Essential Boundary Condition (i.e., Dirichlet Boundary Condition)
We shall illustrate the procedure for the application of the essential boundary condition through an example. For this purpose, consider the example of section 6.5. Here, the mesh consists of N = 6 elements and N +1 = 7 nodes as shown in Fig.7.1.
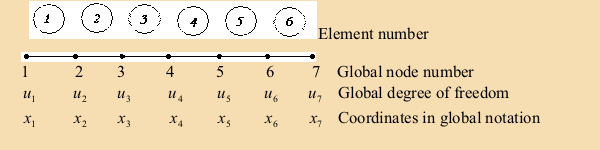
Figure 7.1 Mesh with 6 elements
The approximation over a typical element (shown in Fig 7.2)
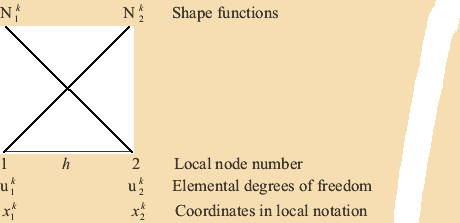
Figure 7.2 Typical element (element No.  ) )
is given by
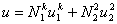 u. u. |
(7.2) |
Here, the shape functions are
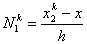 |
|
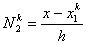 |
(7.3) |
where the element size 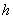 is given by is given by
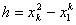 |
(7.4) |
Further it is assumed that the size of all the elements is the same.
Then the global stiffness matrix [ K ] and the global force vector { F } are given by expressions (6.58) and (6.59). Then, the finite element equations become
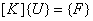 |
(7.5) |
or
Here, P is the point force acting at the right end of the rod. Further, E is the Young's modulus of the rod material, A is the cross sectional area of the rod and 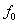 is the distributed axial force acting on the rod, all three being considered as constants. is the distributed axial force acting on the rod, all three being considered as constants.
Suppose, at the left end of the bar, we have the following essential boundary condition :
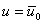 at x = 0. at x = 0. |
(7.7) |
Since we have the first node at the left end (i.e. at 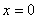 ) where the displacement is denoted by ) where the displacement is denoted by 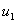 , this boundary condition in terms of the nodal degrees of freedom becomes , this boundary condition in terms of the nodal degrees of freedom becomes
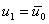 at x = 0. at x = 0. |
(7.8) |
The procedure to apply this boundary condition is described in the next paragraph.
Since the dof 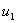 is known, we have only N unknown dof but N +1 algebraic equations. Therefore, one of the equations is redundant. To identify the redundant equation, we proceed as follows. Note that, j th equation of the set (7.6) is obtained by using the weight function is known, we have only N unknown dof but N +1 algebraic equations. Therefore, one of the equations is redundant. To identify the redundant equation, we proceed as follows. Note that, j th equation of the set (7.6) is obtained by using the weight function
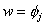 |
(7.9) |
where 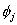 is the j th basis function in the approximation is the j th basis function in the approximation
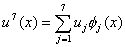 |
(7.10) |
Thus, the first equation of the set (7.6) corresponds to the weight function 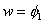 . The weight functions are required to satisfy three admissibility conditions as stated in section 2.2. One of the admissibility requirement is that w should be zero at the boundary where u is specified. Since u is specified at the boundary . The weight functions are required to satisfy three admissibility conditions as stated in section 2.2. One of the admissibility requirement is that w should be zero at the boundary where u is specified. Since u is specified at the boundary 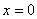 , all the weight functions should be zero at this boundary. However, all the basis functions except , all the weight functions should be zero at this boundary. However, all the basis functions except 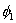 are zero at the boundary are zero at the boundary 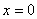 (Fig. 6.1). Thus, (Fig. 6.1). Thus, 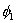 can not be used as the weight function. Therefore, the first equation of set (7.6) is redundant. can not be used as the weight function. Therefore, the first equation of set (7.6) is redundant.
We can actually remove the first equation from the set (7.6) and solve the remaining equations by using the condition 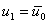 . However, it is not convenient for the computer implementation. Because it involves renumbering the remaining equations and reducing the size of the global stiffness matrix and global force vector. Instead, we replace the redundant first equation by the relation (7.8). Then, equations (7.6) becomes . However, it is not convenient for the computer implementation. Because it involves renumbering the remaining equations and reducing the size of the global stiffness matrix and global force vector. Instead, we replace the redundant first equation by the relation (7.8). Then, equations (7.6) becomes
But now the global coefficient matrix has become unsymmetrical. To restore the symmetry, we transpose the known term 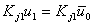 to the right side in the remaining equations ( j = 2,..,7). Then, equation (7.11) becomes to the right side in the remaining equations ( j = 2,..,7). Then, equation (7.11) becomes
The modified equation may be written as
 |
(7.13) |
This equation is solved to get the vector 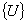 of the unknown dof. Note that the solution gives of the unknown dof. Note that the solution gives 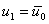 . .
Thus, the algorithm for the application of the essential boundary condition at node 1 is as follows :
- Replace the first equation by the condition
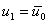 . Thus . Thus
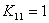 , ,
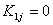 for j = 2,...,7, for j = 2,...,7,
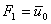 ; ;
|
(7.14) |
- Transpose the known terms from the remaining equations to the right side :
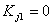 for j = 2,....,7, for j = 2,....,7,
|
|
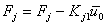 for j = 2,...,7. for j = 2,...,7. |
(7.15) |
When the left end is fixed (i.e., when 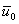 = 0), then = 0), then
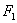 = 0, = 0, |
|
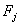 , j = 2,..,N+1 remain unchanged. , j = 2,..,N+1 remain unchanged. |
(7.16) |
Thus, in equation (7.12)
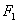 = 0, = 0, |
|
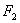 = = 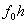 , , |
|
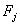 , j = 2,...,7 remain unchanged. , j = 2,...,7 remain unchanged. |
(7.17) |
|