Expressions of Element Stiffness Matrix and Force Vector for Piecewise Quadratic Basis Functions
We use the Galerkin method to develop the finite element equations. Therefore, the integral form to be used is given by equation (2.5b) or (3.68). This equation is rearranged as
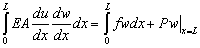 |
(8.19) |
For the Galerkin method, we choose the basis functions 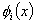 as the weight functions. Thus, as the weight functions. Thus,
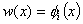 |
for i = 1, 2., Nn |
(8.20) |
where Nn is the number of nodes of the domain. Note that these functions are linearly independent and satisfy all the constraints arising out of the three admissibility conditions on w(x). Substituting the expression (8.20) for w(x) in equation (8.19), we get
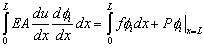 |
for i = 1, 2., Nn |
(8.21) |
Note that the domain (0, L ) is divided into N elements. For kth element, the domain is
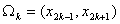 |
|
(8.22) |
(See Fig. 8.3). Substituting the approximation (8.9) for u ( x ) into equation (8.21) and writing the integral from 0 to L as a sum of the N integrals over (2k -1, 2k +1), k = 1,. N , we get the following equations:
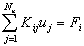 |
for i = 1, 2, 3.., Nn . |
(8.23a) |
In matrix form, this can be written as
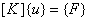 |
(8.23b) |
Here, the stiffness matrix 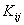 is given by is given by
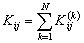 |
for i = 1,2,3.., Nn , for j = 1,2,3.., Nn , |
(8.24) |
where
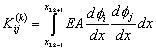 |
for i = 1,2,3.., Nn , for j = 1,2,3.., Nn . |
(8.25) |
Similarly, the force vector 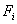 is given by is given by
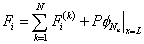 |
for i = 1, 2, 3..., Nn , |
(8.26) |
where
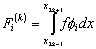 |
for i = 1, 2, 3..., Nn , |
(8.27) |
The derivation of equation (8.23) is similar to the derivations of sections (5.2) and (6.1) for the case of piecewise linear basis functions.
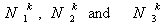 Note that Note that 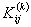 and and 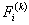 represent the contributions of the kth element to the stiffness matrix represent the contributions of the kth element to the stiffness matrix 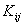 and the force vector and the force vector 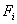 . To simply the expressions (8.25) and (8.27) for . To simply the expressions (8.25) and (8.27) for 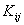 and and 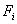 , we note that the only values of ' i ' and ' j ' for which , we note that the only values of ' i ' and ' j ' for which 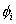 and and 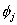 are non-zero over the interval are non-zero over the interval 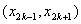 are i = 2k-1, 2k , 2k+1 and j = 2k-1, 2k , 2k +1. Thus, the matrix are i = 2k-1, 2k , 2k+1 and j = 2k-1, 2k , 2k +1. Thus, the matrix 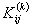 becomes: becomes:
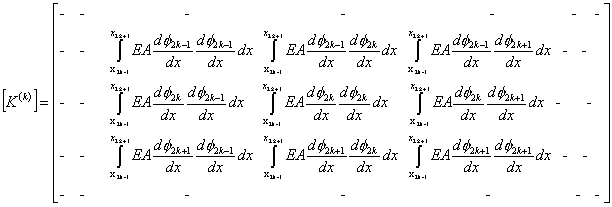
(8.28)
Further, the vector 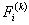 becomes: becomes:
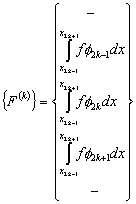 |
|
(8.29) |
Note that the elements of 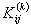 and and 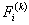 are zero when i ≠ 2k-1, 2k , 2k+1 and j ≠ 2k-1, 2k , 2k+1. Therefore, the matrix are zero when i ≠ 2k-1, 2k , 2k+1 and j ≠ 2k-1, 2k , 2k+1. Therefore, the matrix 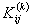 is often condensed as 3x3 matrix with the notation is often condensed as 3x3 matrix with the notation 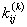 . Similarly the vector . Similarly the vector 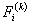 is often condensed as 3x1 vector with the notation is often condensed as 3x1 vector with the notation 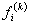 . Next, we use the local notation for the basis functions . Next, we use the local notation for the basis functions 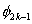 , , 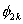 and and 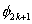 and the coordinates and the coordinates 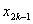 , , 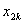 and and 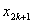 . In local notation, they are written as . In local notation, they are written as 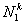 , , 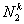 and and 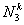 and and 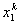 , , 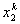 and and 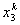 . Then, the condensed form of . Then, the condensed form of 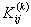 becomes: becomes:
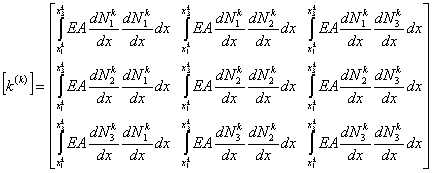 |
(8.30) |
Similarly, the condensed form of 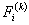 becomes: becomes:
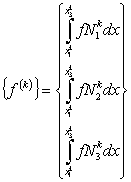 |
(8.31) |
The matrix (8.30) is called as the element stiffness matrix and the vector (8.31) is called as the element force vector. |