Example 1
In the example, the bar of Fig. 3.4 is considered:
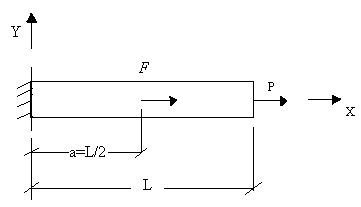
Figure 4.5
The numerical values of various parameters are as before:
| EA = 1 , L = 1 , P = 10 , F = 20. |
(4.7) |
A two-term approximation is chosen for the solution :
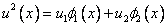 |
(4.8) |
where the functions 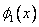 and and 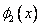 are defined as follows : are defined as follows :
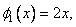 |
for 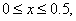 |
|
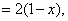
|
for 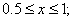 |
(4.9) |
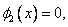 |
for 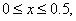 |
|
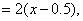 |
for 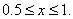 |
(4.10) |
These functions, along with 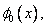 are shown in Fig. 4.6. are shown in Fig. 4.6.
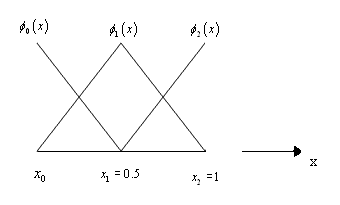
Figure 4.6
Note that the derivatives of the basis functions are given by :
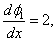 |
for 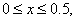 |
|
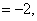
|
for 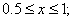 |
(4.11) |
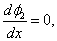 |
for 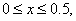 |
|
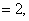 |
for 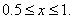 |
(4.12) |
Substituting the expressions (4.11) and (4.12) for 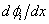 and the values of EI and L from equation (4.7) in equation (3.13), the elements of the stiffness matrix [ K ] become : and the values of EI and L from equation (4.7) in equation (3.13), the elements of the stiffness matrix [ K ] become :
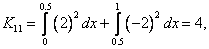 |
(4.13) |
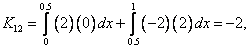 |
(4.14) |
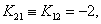 |
(4.15) |
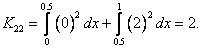 |
(4.16) |
Thus
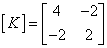 |
(4.17) |
Substituting f = 0 and a = L /2, the expression (3.53) for  becomes : becomes :
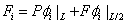 |
(4.18) |
Substituting the values of P , F and L from equation (4.7) and the expressions (4.9) and (4.10) for 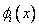 in the above equation, the elements of the force vector become : in the above equation, the elements of the force vector become :
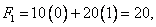
|
(4.19) |
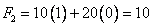 |
(4.20) |
Thus,
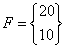 |
(4.21) |
Thus, the algebraic equations (equation 4.6) become :
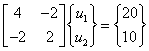 |
(4.22) |
The solution of the above equation is:
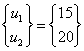 |
(4.23) |
Then, the approximate solution (equation 4.8) becomes :
This is the same as the exact solution (equation 3.65).
The example in the next section shows that, even for a distributed load, the piecewise linear basis functions can approximate the exact solution to any desired level of accuracy.
|