Example 2
In this example, the bar of Fig. 3.1. is considered.
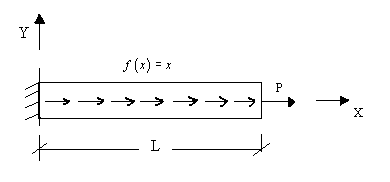
Figure 4.7
The distributed force is given by
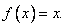 |
(4.25) |
The values of other parameters are the same as before :
| EA = 1 , L = 1 , P = 10. |
(4.26) |
Again, a two term approximation is chosen (equation 4.8) where the basis functions and their derivatives are given by equations (4.9)-(4.12). The basis functions are shown in Fig. 4.6. Since the basis functions and the values of EA and L are the same as in example 1, the [ K ] matrix is the same as before (equation 4.17). With f ( x ) = x , F = 0 and L = 1, the expression (3.53) for 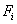 becomes: becomes:
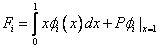 |
(4.27) |
Substituting the expressions (4.9)-(4.10) for 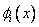 and the value of P from equation (4.26), the elements of the force vector become : and the value of P from equation (4.26), the elements of the force vector become :
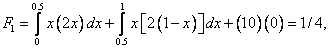
|
(4.28) |
 |
(4.29) |
Thus,
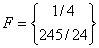 |
(4.30) |
Then, the algebraic equations (equation 4.6) become :
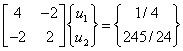 |
(4.31) |
The solution of the above equation is
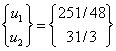 |
(4.32) |
Then, the approximate solution (equation 4.8) becomes :
The exact solution of the problem is given by equation (3.42). The graphical representation of the two solutions ( 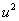 (x) and (x) and 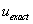 (x)) is shown in Fig. 4.8. (x)) is shown in Fig. 4.8.
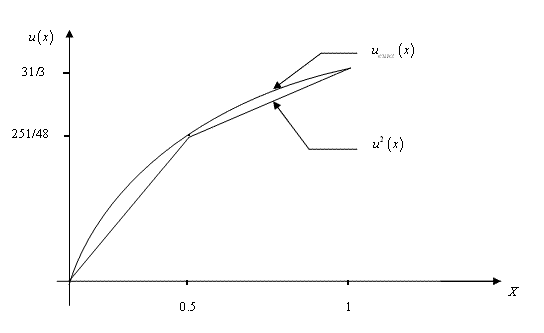
Figure 4.8
If a four-term approximation is chosen
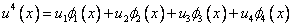 |
(4.34) |
where the basis functions 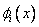 are as shown in Fig. 4.9, are as shown in Fig. 4.9,
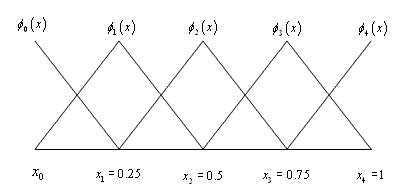
Figure 4.9
then the approximate solution looks like as shown in Fig. 4.10.
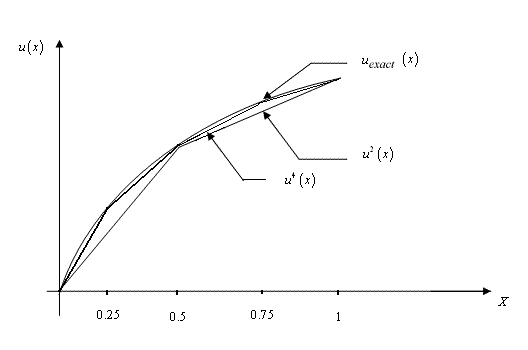
Figure 4.10
Figure 4.10 shows that as we make the approximation finer and finer (i.e., as we add more terms), the solution becomes more and more accurate. Thus, as the number (N) of terms in the approximation increases, 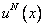 converges to the exact solution. converges to the exact solution.
|