| |
Solution Procedure
As before, an approximate solution is assumed as a series of N+ 1 terms :
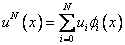 |
(4.1) |
However, here, the unknown coefficients are denoted by 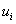 rather than as rather than as 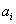 (as in equation 3.2). Note that, the Dirichlet boundary condition (equation 2.1b) implies (as in equation 3.2). Note that, the Dirichlet boundary condition (equation 2.1b) implies
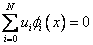 at x = 0 at x = 0 |
(4.2) |
However, all 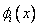 except except 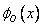 are zero at x = 0 (Fig. 4.3). Therefore, to satisfy this condition, the first coefficient must be zero : are zero at x = 0 (Fig. 4.3). Therefore, to satisfy this condition, the first coefficient must be zero :
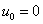 |
(4.3) |
Then, the series (4.2) starts from i = 1 rather than from i = 0. Therefore,
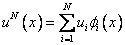 |
(4.4) |
When the expression (4.4) is substituted in the integral form (equation 3.52), we get
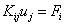 , for i = 1,2,., N , for i = 1,2,., N |
(4.5) |
where the expressions for the stiffness matrix 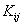 and the force vector and the force vector 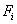 are given by equations (3.13) and (3.53). In matrix form, equation (4.5) can be written as are given by equations (3.13) and (3.53). In matrix form, equation (4.5) can be written as
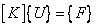 |
(4.6) |
|