Basis Functions
Note that, in the second example of Lecture 3, the exact solution is piecewise linear. Consider another such example shown in Fig. 4.1.
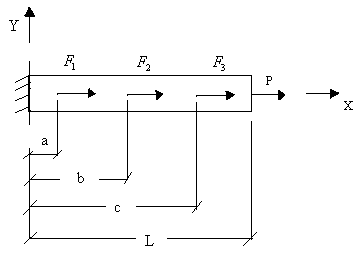
Figure 4.1
Here also, the exact solution is piecewise linear as shown in Fig. 4.2.
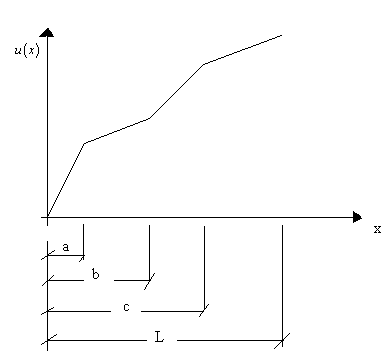
Figure 4.2
This suggests that piecewise linear basis functions may be a better choice in simulating the jumps in the derivatives or providing a more accurate approximation to the derivatives. One such set of ( N +1) functions is shown in Fig. 4.3. To construct such functions, the domain is partitioned into N parts (Fig. 4.3) with the intermediate points 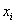 . The functions . The functions 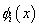 (except (except 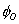 (x) and (x) and 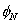 (x)) are zero out side the interval (x)) are zero out side the interval 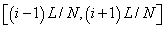 . Within the interval, they are piecewise linear with the maximum value of unity at . Within the interval, they are piecewise linear with the maximum value of unity at 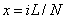 . .
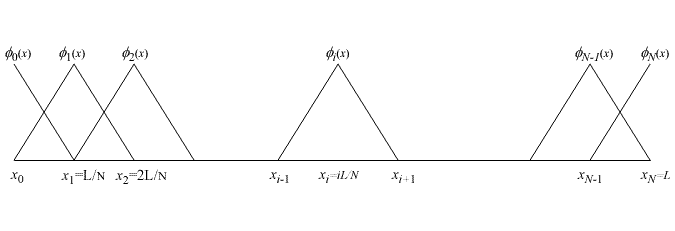
Figure 4.3
Note that these functions are linearly independent and satisfy all the constraints arising out of the three admissibility conditions on u(x). In particular, they satisfy the constraint that the derivatives 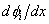 are finite. For are finite. For 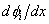 to be finite, the functions to be finite, the functions 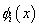 need not be piece-wise linear. They only have to be piecewise differentiable with jumps in the
derivatives as shown in Fig. 4.4. need not be piece-wise linear. They only have to be piecewise differentiable with jumps in the
derivatives as shown in Fig. 4.4. 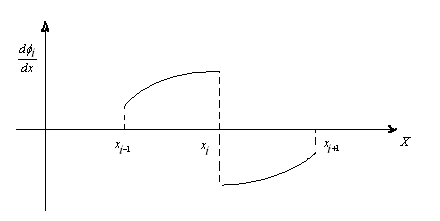
Figure 4.4
|